Cho các số thực a b thỏa mãn a+2b+2c=6. Tìm giá trị lớn nhất của biểu thức: A=ab+ac+2bc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 5 2021
\(\sqrt{2a^2+ab+2b^2}=\sqrt{\dfrac{3}{2}\left(a^2+b^2\right)+\dfrac{1}{2}\left(a+b\right)^2}\ge\sqrt{\dfrac{3}{4}\left(a+b\right)^2+\dfrac{1}{2}\left(a+b\right)^2}=\dfrac{\sqrt{5}}{2}\left(a+b\right)\)
Tương tự:
\(\sqrt{2b^2+bc+2c^2}\ge\dfrac{\sqrt{5}}{2}\left(b+c\right)\) ; \(\sqrt{2c^2+ca+2a^2}\ge\dfrac{\sqrt{5}}{2}\left(c+a\right)\)
Cộng vế với vế:
\(P\ge\sqrt{5}\left(a+b+c\right)\ge\dfrac{\sqrt{5}}{3}\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^3=\dfrac{\sqrt{5}}{3}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{9}\)
CM
29 tháng 11 2018
Đáp án B
Áp dụng bất đẳng thức giá trị tuyệt đối và bất đẳng thức BCS, ta có kết quả sau:
2 a + b - 2 c + 7 = 2 a + 1 + b - 2 - 2 c + 11 ≤ 2 a - 1 + b - 2 - 2 c + 11 ≤ a - 1 2 + b - 2 2 + c 2 2 2 + 1 2 + - 2 2 + 11 = 20
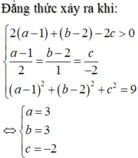
Cách 2: phương pháp hình học.
Trong không gian Oxyz, gọi mặt cầu (S) có tâm I(1;2;0), bán kính R=3. Khi đó:
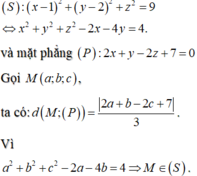
Bài toán đã cho trở thành:
Tìm M ∈ ( S ) sao cho d(M;(P)) lớn nhất
Gọi △ là đường thẳng qua I và vuông góc (P)
Phân tích: Khi quan sát 2 cách giải, đối với giáo viên ta sẽ dễ chọn Cách 1 vì ngắn gọn và tiết kiệm thời gian. Tuy nhiên học sinh không nhiều em đã từng được tiếp cận bất đẳng thức BCS. Đối với Cách 2, về mặt trình bày có thể dài hơi, nhiều tính toán hơn nhưng đó chỉ là những bước tính toán khá cơ bản, một học sinh khá nếu nhận ra ý đồ tác giả thì việc giải bài toán cũng không mất quá nhiều thời gian. Bài toán sẽ dễ hơn nếu đề bài chỉ yêu cầu tìm Min hoặc Max của biểu thức 2 a + b - 2 c + 7
20 tháng 8 2023
Ta có \(ab+bc+ca=3abc\)
\(\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(x=\dfrac{1}{a},y=\dfrac{1}{b},z=\dfrac{1}{c}\) thì ta có \(x,y,z>0;x+y+z=3\) và
\(\sqrt{\dfrac{a}{3b^2c^2+abc}}=\sqrt{\dfrac{\dfrac{1}{x}}{3.\dfrac{1}{y^2z^2}+\dfrac{1}{xyz}}}=\sqrt{\dfrac{\dfrac{1}{x}}{\dfrac{3x+yz}{xy^2z^2}}}=\sqrt{\dfrac{y^2z^2}{3x+yz}}\) \(=\dfrac{yz}{\sqrt{3x+yz}}\) \(=\dfrac{yz}{\sqrt{x\left(x+y+z\right)+yz}}\) \(=\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}\)
Do đó \(T=\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}+\dfrac{zx}{\sqrt{\left(y+z\right)\left(y+x\right)}}+\dfrac{xy}{\sqrt{\left(z+x\right)\left(z+y\right)}}\)
Lại có \(\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}\le\dfrac{yz}{2\left(x+y\right)}+\dfrac{yz}{2\left(x+z\right)}\)
Lập 2 BĐT tương tự rồi cộng theo vế, ta được \(T\le\dfrac{yz}{2\left(x+y\right)}+\dfrac{yz}{2\left(x+z\right)}+\dfrac{zx}{2\left(y+z\right)}+\dfrac{zx}{2\left(y+x\right)}\) \(+\dfrac{xy}{2\left(z+x\right)}+\dfrac{xy}{2\left(z+y\right)}\)
\(T\le\dfrac{yz+zx}{2\left(x+y\right)}+\dfrac{xy+zx}{2\left(y+z\right)}+\dfrac{xy+yz}{2\left(z+x\right)}\)
\(T\le\dfrac{x+y+z}{2}\) (do \(x+y+z=3\))
\(T\le\dfrac{3}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=1\) \(\Leftrightarrow a=b=c=1\)
Vậy \(maxT=\dfrac{3}{2}\), xảy ra khi \(a=b=c=1\)
(Mình muốn gửi lời cảm ơn tới bạn Nguyễn Đức Trí vì ý tưởng của bài này chính là bài mình vừa hỏi lúc nãy trên diễn đàn. Cảm ơn bạn Trí rất nhiều vì đã giúp mình có được lời giải này.)
ND
Nguyễn Đức Trí
VIP
20 tháng 8 2023
Bạn Lê Song Phương xem lại dùm nhé, thanks!
\(...\dfrac{yz}{\sqrt[]{\left(x+y\right)\left(x+z\right)}}\le\dfrac{2yz}{x+y}+\dfrac{2yz}{x+z}\)
\(...\Rightarrow T\le2.3=6\)
\(\Rightarrow GTLN\left(T\right)=6\left(tạia=b=c=1\right)\)
NB
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
9 tháng 11 2023
1/\(=4a^2+4b^2+c^2+8ab-4bc-4ca+4b^2+4c^2+a^2+8bc-4ca-4ab+4a^2+4c^2+b^2+8ca-4bc-4ab=\)
\(=9a^2+9b^2+9c^2=9\left(a^2+b^2+c^2\right)\)
2/
Ta có
\(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge-2\left(ab+bc+ca\right)=2\)
\(\Rightarrow P=9\left(a^2+b^2+c^2\right)\ge18\)
\(\Rightarrow P_{min}=18\)
Vì \(a+2b+2c=6\)
\(\Rightarrow2\left(b+c\right)=6-a\Leftrightarrow b+c=\frac{6-a}{2}\)
Thay vào A:
\(A=ab+ac+2bc=a\left(b+c\right)+2bc\)
\(\le a\left(b+c\right)+\frac{\left(b+c\right)^2}{2}=\frac{a\left(6-a\right)}{2}+\frac{\left(\frac{6-a}{2}\right)^2}{2}\)
\(=\frac{-3a^2+12a+36}{8}=\frac{-3\left(a^2-4a+4\right)+48}{8}=\frac{-3\left(a-2\right)^2}{8}+6\le6\)
Vậy GTLN của A = 6 khi a = 2; b = c = 1