Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)

=>\(\dfrac{AC}{AB}=\sqrt{3}\)

=>\(\dfrac{AC^2}{AB^2}=3\)

=>\(AC^3=3AB^2\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(4\cdot AB^2=2^2=4\)

=>\(AB^2=1\)

=>AB=1(cm)

=>\(AC=1\cdot\sqrt{3}=\sqrt{3}\left(cm\right)\)

a: Xét (O) có

ΔCMD nội tiếp

CD là đường kính

Do đó:ΔCMD vuông tại M

=>DM\(\perp\)CF tại M

b: Xét (O) có AB,CD là các đường kính và AB\(\perp\)CD tại O

nên \(sđ\stackrel\frown{CA}=sđ\stackrel\frown{CB}=sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD}\)

Xét (O) có \(\widehat{MNB}\) là góc có đỉnh ở bên trong đường tròn chắn hai cung MB,AD

=>\(\widehat{MNB}=\dfrac{1}{2}\left(sđ\stackrel\frown{MB}+sđ\stackrel\frown{AD}\right)=\dfrac{1}{2}\left(sđ\stackrel\frown{MB}+sđ\stackrel\frown{BD}\right)=\dfrac{1}{2}\cdot sđ\stackrel\frown{MD}\)

Xét (O) có

\(\widehat{DME}\) là góc tạo bởi tiếp tuyến ME và dây cung MD

=>\(\widehat{DME}=\dfrac{1}{2}\cdot sđ\stackrel\frown{MD}\)

=>\(\widehat{DME}=\widehat{MNB}\)

=>ΔENM cân tại E

Ta có: \(\widehat{EMN}+\widehat{EMF}=\widehat{FMN}=90^0\)

\(\widehat{ENM}+\widehat{EFM}=90^0\)(ΔNMF vuông tại M)

mà \(\widehat{ENM}=\widehat{EMN}\)

nên \(\widehat{EMF}=\widehat{EFM}\)

=>ΔEFM cân tại E

a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)

=>\(BH\cdot BC=BA^2\)

b: Xét ΔAHB vuông tại H có HD là đường cao

nên \(AD\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HE là đường cao

nên \(AE\cdot AC=AH^2\left(2\right)\)

Từ (1),(2) suy ra \(AD\cdot AB=AE\cdot AC\)

=>\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)

Xét ΔADE vuông tại A và ΔACB vuông tại A có

\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)

Do đó: ΔADE~ΔACB

đéo

Tâm nhĩ co để đẩy máu lên phổi lấy oxi rồi đưa lại về tim, trong khi tâm nhĩ co để đẩy máu giàu oxi đi nuôi khắp cơ thể nên lực co bóp phải mạnh và chậm hơn so với tâm nhĩ co. Như vậy do đường đi của máu từ tâm thất dài hơn đường đi của máu từ tâm nhĩ nên thời gian co bóp lâu hơn, lực mạch hơn.

từ (a+b+c)^2=a^2+b^2+c^2

suy ra ab+bc+ac=0suy ra ab=-(bc+ac);ac=-(ab+bc);bc=-(ab+ac)

xét a^2+2bc=a^2+bc-ab-ac=(a-c)(a-b)

tương tự dc b^2+2ac=(b-a)(b-c)

c^2+2ab=(a-c)(b-c)

thay vao điều phải c/m dc 

a^2/(a-c)(a-b)  -b^2/(a-b)(b-c)   +c^2(a-c)(b-c)    

=a^2b-a^2c-b^2a+b^2c+c^2a-bc^2/(a-b)(a-c)(b-c)

=abc(ac-bc+bc-ab+ab-ac)/(a-b)(a-c)(b-c)=0 

Xét tam giác ABC vuông tại A

a, Theo Pytago ta có \(c=\sqrt{a^2-b^2}=3\sqrt{13}\)

sinB = AC/BC = 18/21 = 6/7 => ^B = \(\approx\)59⁰

Do ^B ; ^C phụ nhau => ^C \(\approx\)31⁰

b, Do ^B ; ^C phụ nhau => ^B = 60⁰

tanC = AB/AC = c/b => c = b.tanC = \(\dfrac{10\sqrt{3}}{3}\)

cosC = AC/BC = b/a => a = b/cosC = \(\dfrac{20\sqrt{3}}{3}\)

c, Theo Pytago \(a=\sqrt{b^2+c^2}=\sqrt{34}\)

tanB = AC/AB => ^B  \(\approx\)31⁰ 

Do ^B ; ^C phụ nhau ^C \(\approx\)59⁰

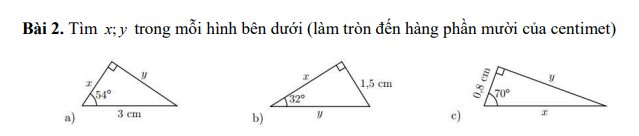
a) Ta có: 

\(sin54^o=\dfrac{y}{3}=>y=3\cdot sin54^o\approx2,4\left(cm\right)\\ =>x=\sqrt{3^2-y^2}=\sqrt{9-2,4^2}\approx1,8\left(cm\right)\)

b) Ta có: 

\(sin32^o=\dfrac{1,5}{y}=>y=\dfrac{1,5}{sin32^o}\approx2,8\left(cm\right)\\ =>x=\sqrt{y^2-1,5^2}=\sqrt{2,8^2-1,5^2}\approx2,4\) 

c) Ta có:

\(tan70^o=\dfrac{y}{0,8}=>y=0,8\cdot tan70^o\approx2,2\left(cm\right)\\ =>x=\sqrt{y^2+0,8^2}=\sqrt{2,2^2+0,8^2}\approx2,3\left(cm\right)\)

Cho tam giác ABC vuông tại A, ^B là góc biết số đo 

a, sinB = y/3 => y  \(\approx\)2,42 cm 

cosB = x/3 => y \(\approx\)1,76 cm 

b, sinB = 1,5/y => y = 1,5/sinB \(\approx\)2,83 cm 

tanB = 1,5/x => x = 1,5/tanB => x \(\approx\)2,4 cm 

c, tanB = y/0,8 => y = 0,8.tanB => y \(\approx\)2,19 cm 

cosB = 0,8/x => x = 0,8/cosB => x \(\approx\)2,34 cm