Thưa thầy/cô, em còn nhớ những buổi học đầu tiên, khi em còn bỡ ngỡ và lo lắng. Nhờ có thầy/cô luôn bên cạnh động viên, hướng dẫn, em đã dần tự tin hơn. Em xin gửi lời cảm ơn chân thành đến thầy/cô, những người đã dìu dắt em từng bước trên con đường học tập.
Nhân ngày Nhà giáo Việt Nam 20/11, em xin kính chúc thầy/cô luôn mạnh khỏe, tràn đầy năng lượng để tiếp tục sự nghiệp trồng người cao quý. Chúc thầy/cô luôn vui vẻ, hạnh phúc bên gia đình và bạn bè. Em luôn ngưỡng mộ sự tận tâm, nhiệt huyết của thầy/cô. Thầy/cô không chỉ là người thầy mà còn là người bạn, người truyền cảm hứng cho em.
Nhờ những kiến thức và kỹ năng mà thầy/cô truyền dạy, em đã có thể tự tin tham gia các hoạt động của trường lớp. Em sẽ cố gắng học tập thật tốt để không phụ lòng thầy/cô. Em mong muốn sau này sẽ trở thành một người có ích cho xã hội, giống như thầy/cô vậy.
Một lần nữa, em xin gửi lời cảm ơn sâu sắc đến thầy/cô. Em sẽ mãi ghi nhớ công ơn của thầy/cô. Chúc thầy/cô một ngày 20/11 thật ý nghĩa và hạnh phúc.

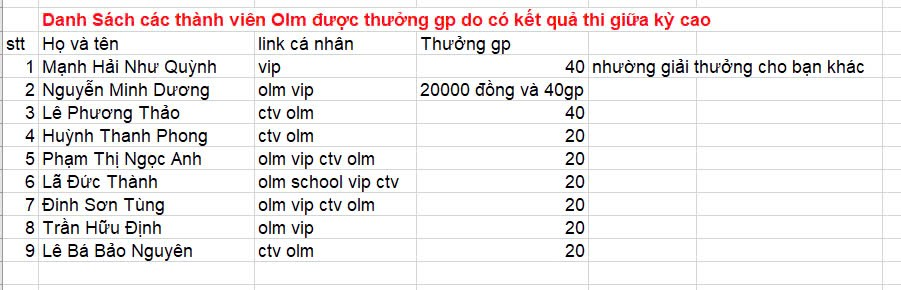
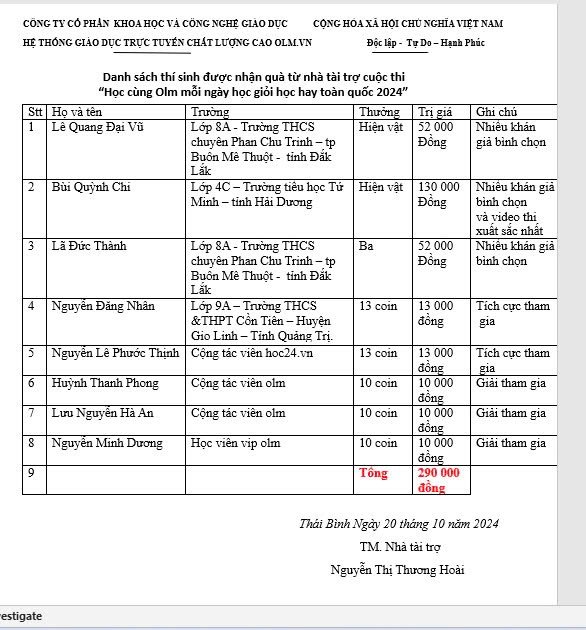
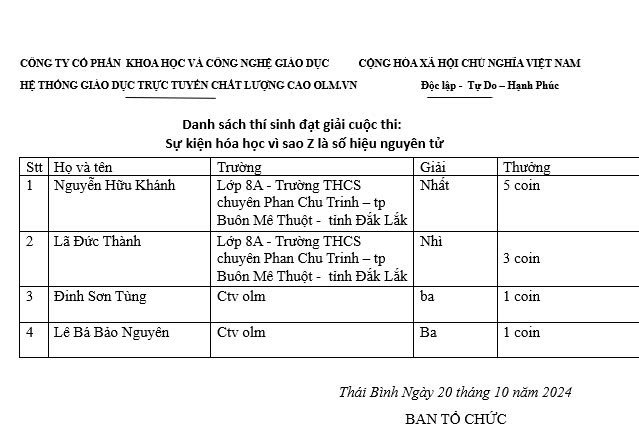
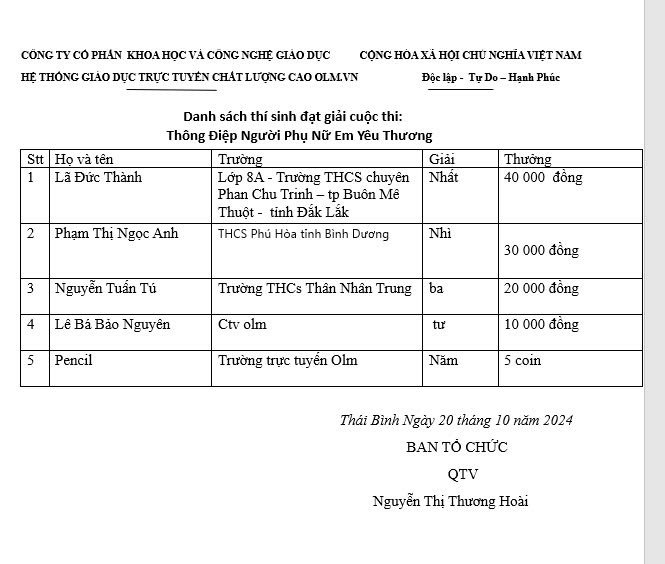

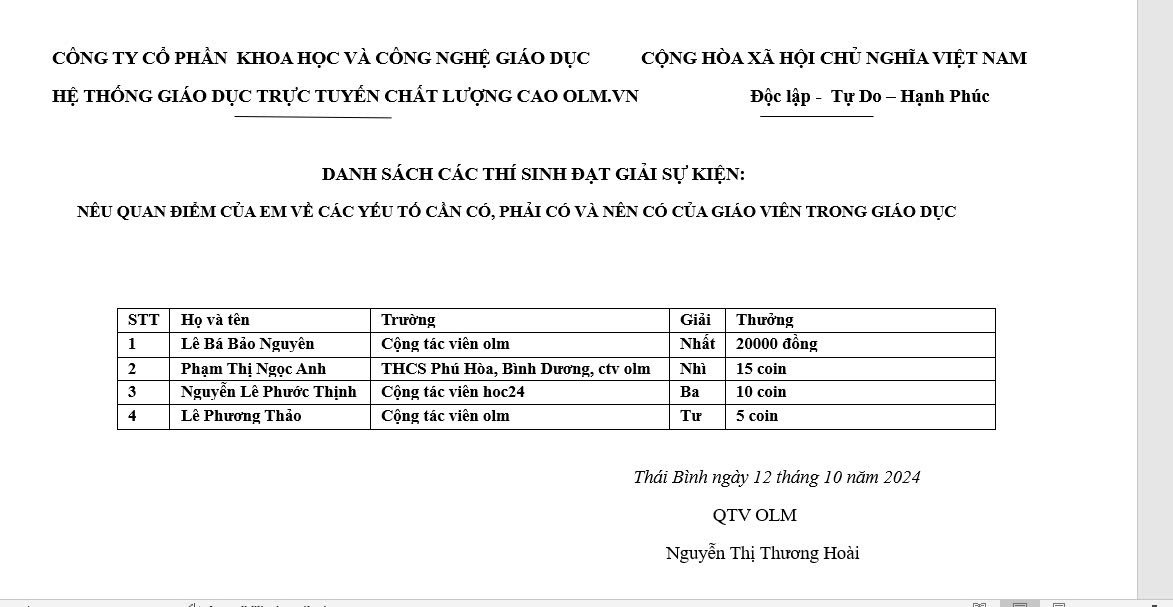
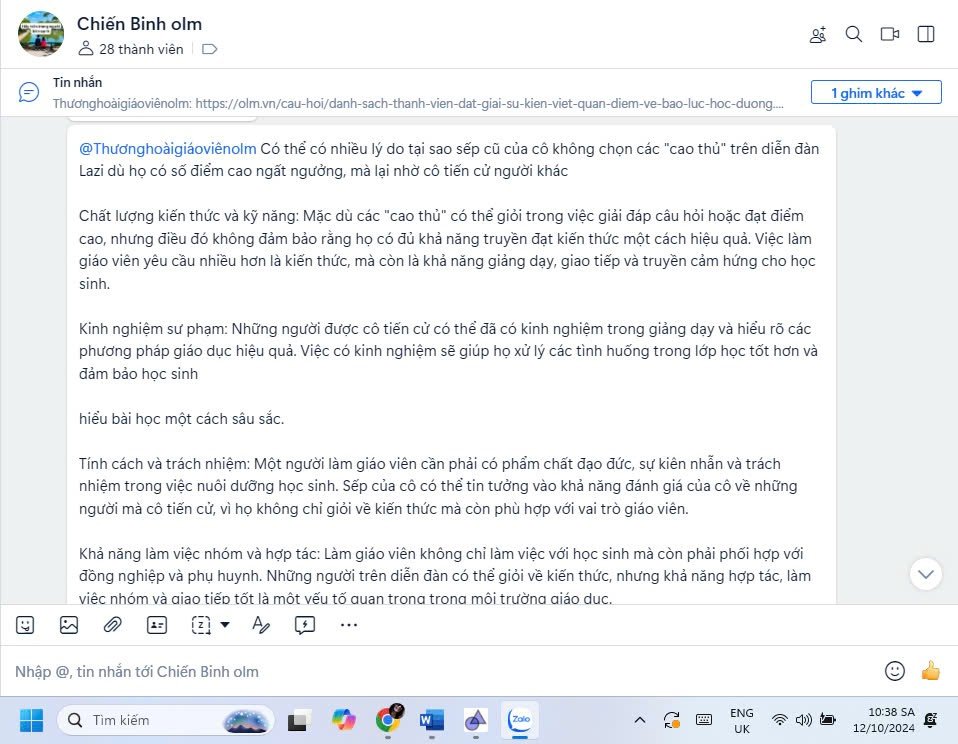
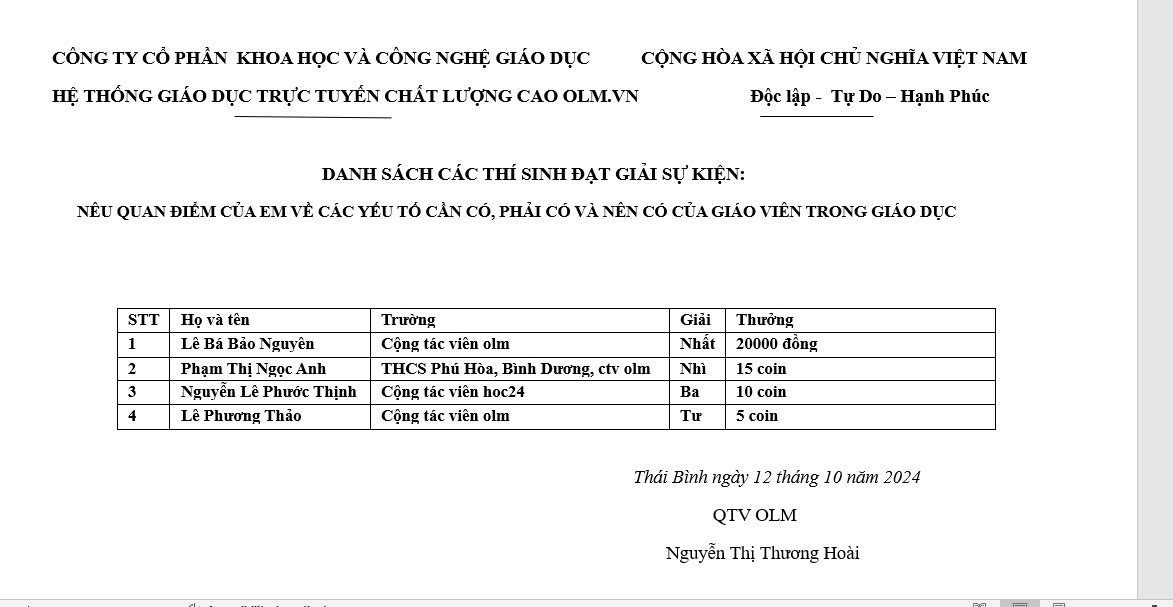
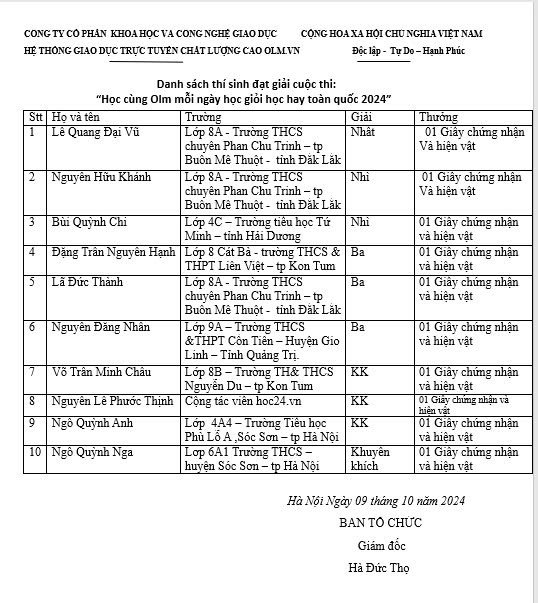
Thay mặt thầy cô giáo cũng như tập thể đội ngũ những người đang hoạt động trong lĩnh vực giáo dục cảm ơn những lời chúc và những tình cảm tốt đẹp mà em đã giành cho thầy cô nói chung và Olm nói riêng. Chúc em luôn mạnh khỏe, an nhiên, bình yên trong cuộc sống, nỗ lực và cố gắng học tập để trở thành những chủ nhân tương lai đất nước tài đức vẹn toàn.