Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

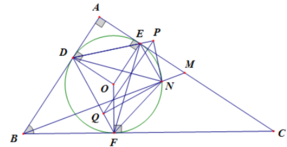
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.

a) Xét đường tròn (J1) có: ^HJ1D = 2.^HMD (^HMD=1/2.Sđ(HD ). Tương tự: ^KJ2D = 2.^KND
Dễ thấy tứ giác MEFN nội tiếp (Do ^MEN = ^MFN) => ^DMH = ^DNK (2 góc nội tiếp cùng chắn cung EF)
Do đó: ^HJ1D = ^KJ2D. Mà các tam giác HJ1D và KJ2D cân tại J1 và J2 => ^J2DK + 1/2.^HJ1D = 900
Hay ^J2DK + ^HMD = 900 => J2D vuông góc EM. Có J1H vuông góc EM => J2D // J1H
=> ^J1DJ2 = ^HJ1D (So le trong) => ^HDK = ^J1DJ2 + ^J1DH + ^J2DK = ^HJ1D + ^J1DH + ^J1HD = 1800
=> 3 điểm K,H,D thẳng hàng. Lại có: ^AHD = 1/2.Sđ(HD; ^AKD = 1/2.Sđ(KD => ^AHD = ^AKD
Từ đó: ^AHK = ^AKH => \(\Delta\)HAK cân tại A => AH=AK
Gọi giao điểm của tia AD với (I1) và (J1) lần lượt là P' và Q'. Ta sẽ chứng minh P' trùng P; Q' trùng Q.
Theo hệ thức lượng trong đường tròn: AH2 = AD.AQ' => AK2 = AD.AQ' => \(\Delta\)ADK ~ \(\Delta\)AKQ' (c.g.c)
=> ^AKD = ^AQ'K = 1/2.Sđ(DK => Điểm Q' nằm trên (J2) => Q' trùng Q (1)
Tương tự: AE.AM = AD.AP'; AE.AM = AF.AN => AF.AN = AD.AP' => \(\Delta\)ADF ~ \(\Delta\)ANP' (c.g.c)
=> ^ADF = ^ANP' => Tứ giác DFNP' nột tiếp => Điểm P' thuộc (DFN) hay P' thuộc (I2) => P' trùng P (2)
Từ (1) và (2) => Tia AD đi qua 2 điểm P và Q hay 3 điểm D,P,Q thẳng hàng (đpcm).
b) Định trên đoạn thẳng EF một điểm T thỏa mãn \(\frac{ET}{FT}=\frac{HD}{KD}\)
Ta thấy ^GEA = ^GFA => ^GEH = ^GFK. Kết hợp với ^GHE = ^GKF => \(\Delta\)GEH ~ \(\Delta\)GFK (g.g)
=> \(\frac{GE}{GH}=\frac{GF}{GK}\). Lại có: ^EGF = ^EAF = ^HGK (Các góc nội tiếp) => \(\Delta\)GEF ~ \(\Delta\)GHK (c.g.c)
Do T và D định trên các cạnh EF, HK các tỉ số tương ứng bằng nhau nên \(\Delta\)GTF ~ \(\Delta\)GDK (c.g.c)
=> \(\frac{GT}{GD}=\frac{GF}{GK}\). Nhưng ^TGD = ^FGK (=^TGF - ^TGK) nên \(\Delta\)GTD ~ \(\Delta\)GFK (c.g.c)
=> ^GDT = ^GKF. Mà ^GKF = ^GQD => ^GDT = ^GQD = 1/2.Sđ(GD => DT là tia tiếp tuyến của đường tròn (DGQ) (3)
Mặt khác:^GLE = ^GFE = ^GKH = ^GQH. Dễ thấy: \(\Delta\)LEF ~ \(\Delta\)QHK. Từ \(\frac{ET}{FT}=\frac{HD}{KD}\)=> \(\Delta\)ELT ~ \(\Delta\)HQD
=> ^ELT = ^HQD => ^ELT - ^GLE = ^HQD - ^GQH => ^GLT = ^GQD. Mà ^GQD = ^GDT (cmt) nên ^GLT = ^GDT
Từ đó có: Tứ giác GDLT nội tiếp hay điểm T nằm trên đường tròn (DLG) (4)
Qua (3) và (4) suy ra: Tiếp tuyến tại D của đường tròn (DGQ) cắt EF tại điểm T nằm trên đường tròn (DLG) (đpcm).

4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.

Vì N là điểm chính giữa cung nhỏ BC nên DN là trung trực của BC nên DN là phân giác B D C ^
Ta có K Q C ^ = 2 K M C ^ (góc nọi tiếp bằng nửa góc ở tâm trong dường tròn (Q))
N D C ^ = K M C ^ (góc nội tiếp cùng chắn cung N C ⏜ )
Mà B D C ^ = 2 N D C ^ ⇒ K Q C ^ = B D C ^
Xét 2 tam giác BDC & KQC là các các tam giác vuông tại D và Q có hai góc ở ⇒ B C D ^ = B C Q ^ do vậy D, Q, C thẳng hàng nên KQ//PK
Chứng minh tương tự ta có ta có D, P, B thẳng hàng và DQ//PK
Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng (điều phải chứng minh).
a. Từ N kẻ đường thẳng vuông góc với AB, cắt OM tại I. Vậy (I; IN) chính là tâm đường tròn cần tìm.
Ta chỉ cần chứng minh M thuộc (I). Thật vậy, IN // KO (Cùng vuông góc AB) nên \(\widehat{OKM}=\widehat{INM}\) mà \(\widehat{OKM}=\widehat{OMK}\)
Vậy nên \(\widehat{IMN}=\widehat{INM}\Rightarrow IN=IM\). Vậy M thuộc đường tròn (I).
b. Kẻ tiếp tuyến Mx của hai đường tròn. Khi đó \(\widehat{FEM}=\widehat{FMx}=\widehat{BMx}=\widehat{BAM}\)
Chúng lại ở vị trí so le trong nên EF // AB.
c. Ta thấy ngay \(\Delta OKN\sim\Delta KMJ\left(g-g\right)\Rightarrow\frac{KN}{MJ}=\frac{OK}{KM}\Rightarrow KM.KN=MJ.OK=2R^2.\)
d. Coi AK = 1, đặt \(\frac{NB}{AB}=t\Rightarrow\frac{AN}{AB}=1-t;NP=t;NQ=1-t;PQ=\sqrt{t^2+\left(1-t\right)^2}\)
Ta tìm min \(1+\sqrt{2t^2-2t+1}=1+\sqrt{2\left(t-\frac{1}{2}\right)^2+\frac{1}{2}}\ge1+\frac{1}{\sqrt{2}}\)
Dấu bằng xảy ra khi \(t=\frac{1}{2}\) hay N trùng O.
tks bạn nha !