Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
\(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\)
\(\Leftrightarrow x^2y^2\left(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)\ge\dfrac{4}{xy}.x^2y^2\)
\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2+y^2\ge4xy\)
\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2-2xy+y^2\ge2xy\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2+\left(x-y\right)^2\ge2xy\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2-2xy+\left(x-y\right)^2\ge0\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}-x+y\right)^2=0\) (luôn đúng)

Lời giải:
Xét hiệu:
\(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}-\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)\)
\(=\frac{a-c}{b}+\frac{b-a}{c}+\frac{c-b}{a}=-\frac{(b-a)+(c-b)}{b}+\frac{b-a}{c}+\frac{c-b}{a}\)
\(=\frac{b-a}{c}-\frac{b-a}{b}+\frac{c-b}{a}-\frac{c-b}{b}\)
\(=(b-a)(\frac{1}{c}-\frac{1}{b})+(c-b)(\frac{1}{a}-\frac{1}{b})\)
\(=\frac{(b-a)(b-c)}{bc}+\frac{(c-b)(b-a)}{ab}=(b-a)(b-c)(\frac{1}{bc}-\frac{1}{ab})\)
\(=\frac{(b-a)(b-c)(a-c)}{abc}\geq 0\) do \(0\leq a\leq b\leq c\)
Do đó:
\(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\geq \frac{b}{a}+\frac{c}{b}+\frac{a}{c}\) (đpcm)
Dấu bằng xảy ra khi $a=b=c$

a) Áp dụng bất đẳng thức AM-GM ta có:
\(\dfrac{bc}{a}+\dfrac{ac}{b}\ge2\sqrt{\dfrac{abc^2}{ab}}=2\sqrt{c^2}=2\left|c\right|=2c\left(c>0\right)\)
Chứng minh tương tự ta được: \(\left\{{}\begin{matrix}\dfrac{ac}{b}+\dfrac{ab}{c}\ge2a\\\dfrac{bc}{a}+\dfrac{ab}{c}\ge2b\end{matrix}\right.\)
Cộng theo vế: \(\dfrac{bc}{a}+\dfrac{ac}{b}+\dfrac{ab}{c}\ge a+b+c\left(đpcm\right)\)
Áp dụng liên tiếp AM-GM và Cauchy-Schwarz ta được:
\(\dfrac{ab}{a+b}=\dfrac{ab+b^2-b^2}{a+b}=\dfrac{b\left(a+b\right)}{a+b}-\dfrac{b^2}{a+b}=b-\dfrac{b^2}{a+b}\)
Chứng minh tương tự:
\(\left\{{}\begin{matrix}\dfrac{bc}{b+c}=\dfrac{bc+c^2-c^2}{b+c}=\dfrac{c\left(b+c\right)}{b+c}-\dfrac{c^2}{b+c}=c-\dfrac{c^2}{b+c}\\\dfrac{ac}{c+a}=\dfrac{ac+a^2-a^2}{c+a}=\dfrac{a\left(c+a\right)}{c+a}-\dfrac{a^2}{c+a}=a-\dfrac{a^2}{c+a}\end{matrix}\right.\)
Cộng theo vế:
\(\dfrac{ab}{a+b}+\dfrac{bc}{b+c}+\dfrac{ac}{a+c}=a+b+c-\left(\dfrac{b^2}{a+b}+\dfrac{c^2}{b+c}+\dfrac{a^2}{a+c}\right)\le\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=a+b+c-\dfrac{a+b+c}{2}=\dfrac{a+b+c}{2}\left(đpcm\right)\)
b)Đặt \(A=\dfrac{ab}{a+b}+\dfrac{bc}{b+c}+\dfrac{ca}{c+a}\)
\(A=\dfrac{a\left(a+b\right)-a^2}{a+b}+\dfrac{b\left(b+c\right)-b^2}{a+b}+\dfrac{c\left(c+a\right)-c^2}{c+a}\)
\(A=a+b+c-\dfrac{a^2}{a+b}-\dfrac{b^2}{b+c}-\dfrac{c^2}{c+a}\)
Lại có:\(\dfrac{a^2}{a+b}+\dfrac{b^2}{b+c}+\dfrac{c^2}{c+a}\ge\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=\dfrac{a+b+c}{2}\)
\(\Rightarrow A\le a+b+c-\dfrac{a+b+c}{2}=\dfrac{a+b+c}{2}\)
\(\Rightarrowđpcm\)

Ta có : \(a^2+b^2\ge2ab\Rightarrow a^2+b^2-ab\ge ab\)
\(\Rightarrow\dfrac{1}{a^2-ab+b^2}\le\dfrac{1}{ab}=\dfrac{abc}{ab}=c\) ( do $abc=1$ )
Tương tự ta có :
\(\dfrac{1}{b^2-bc+c^2}\le a\)
\(\dfrac{1}{c^2-ab+a^2}\le b\)
Cộng vế với vế các BĐT trên có :
\(\dfrac{1}{a^2-ab+b^2}+\dfrac{1}{b^2-bc+c^2}+\dfrac{1}{c^2-ac+a^2}\le a+b+c\)
Dấu "=" xảy ra khi $a=b=c$
\(VT=\dfrac{1}{a^2+b^2-ab}+\dfrac{1}{b^2+c^2-bc}+\dfrac{1}{c^2+a^2-ca}\)
\(VT\le\dfrac{1}{2ab-ab}+\dfrac{1}{2bc-bc}+\dfrac{1}{2ca-ca}=\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}=\dfrac{a+b+c}{abc}=a+b+c\)
Dấu "=" xảy ra khi \(a=b=c=1\)
cho ba số dương \(0\le a\le b\le c\le1\) CMR \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le2\)

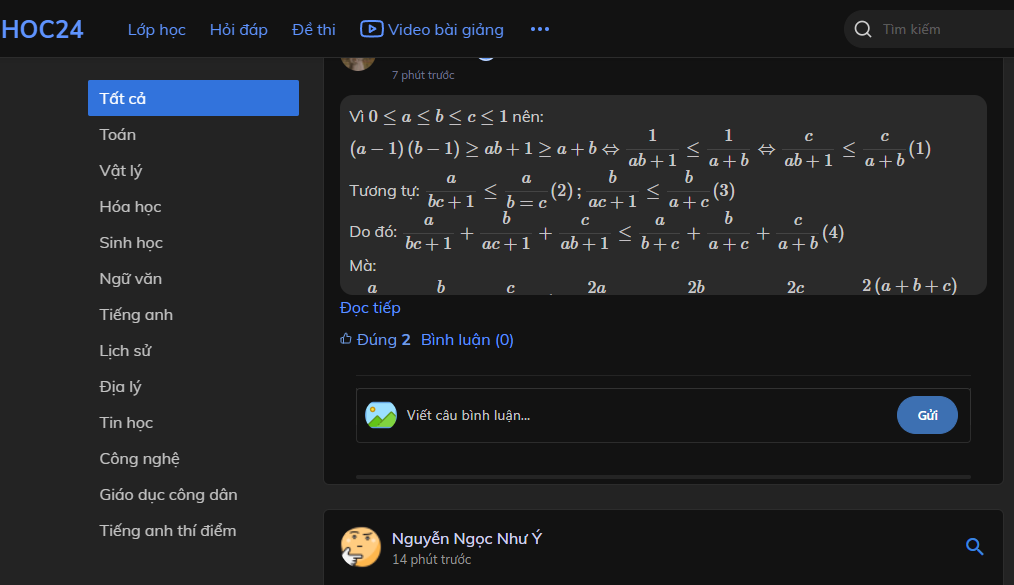
Vì \(0\le a\le b\le c\le1\) nên:
\(\left(a-1\right)\left(b-1\right)\ge ab+1\ge a+b\Leftrightarrow\dfrac{1}{ab+1}\le\dfrac{1}{a+b}\Leftrightarrow\dfrac{c}{ab+1}\le\dfrac{c}{a+b}\left(1\right)\)
Tương tự: \(\dfrac{a}{bc+1}\le\dfrac{a}{b=c}\left(2\right);\dfrac{b}{ac+1}\le\dfrac{b}{a+c}\left(3\right)\)
Do đó: \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\left(4\right)\)
Mà: \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\le\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(5\right)\)
Từ (4) và (5) suy ra \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\left(đpcm\right)\)

Đặt vế trái BĐT cần chứng minh là P
Ta có:
\(P=\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{a^2}{\sqrt{2\left(b^2+c^2\right)}}+\dfrac{b^2}{\sqrt{2\left(a^2+c^2\right)}}+\dfrac{c^2}{\sqrt{2\left(a^2+b^2\right)}}\)
Đặt \(\left(\sqrt{b^2+c^2};\sqrt{c^2+a^2};\sqrt{a^2+b^2}\right)=\left(x;y;z\right)\Rightarrow x+y+z=\sqrt{2011}\)
Đồng thời: \(\left\{{}\begin{matrix}y^2+z^2-x^2=2a^2\\z^2+x^2-y^2=2b^2\\x^2+y^2-z^2=2c^2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{y^2+z^2-x^2}{2}\\b^2=\dfrac{z^2+x^2-y^2}{2}\\c^2=\dfrac{x^2+y^2-z^2}{2}\end{matrix}\right.\)
\(\Rightarrow P\ge\dfrac{1}{2\sqrt{2}}\left(\dfrac{y^2+z^2-x^2}{x}+\dfrac{z^2+x^2-y^2}{y}+\dfrac{x^2+y^2-z^2}{z}\right)\)
\(\Rightarrow P\ge\dfrac{1}{2\sqrt{2}}\left(\dfrac{y^2+z^2}{x}+\dfrac{z^2+x^2}{y}+\dfrac{x^2+y^2}{z}-\left(x+y+z\right)\right)\)
\(\Rightarrow P\ge\dfrac{1}{2\sqrt{2}}\left(\dfrac{\left(y+z\right)^2}{2x}+\dfrac{\left(z+x\right)^2}{2y}+\dfrac{\left(x+y\right)^2}{2z}-\left(x+y+z\right)\right)\)
\(\Rightarrow P\ge\dfrac{1}{2\sqrt{2}}\left(\dfrac{\left(y+z+z+x+x+y\right)^2}{2x+2y+2z}-\left(x+y+z\right)\right)=\dfrac{1}{2\sqrt{2}}\left(x+y+z\right)=\dfrac{1}{2}\sqrt{\dfrac{2011}{2}}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\sqrt{\dfrac{2011}{2}}\)

Áp dụng bất đẳng thức Cauchy-Schwarz:
\(A=\dfrac{1}{1+ab}+\dfrac{1}{1+bc}+\dfrac{1}{1+ca}\)
\(A\ge\dfrac{\left(1+1+1\right)^2}{3+ab+bc+ac}=\dfrac{9}{3+ab+bc+ac}\)
Mặt khác,theo hệ quả AM-GM: \(ab+bc+ac\le\dfrac{\left(a+b+c\right)^2}{3}\le\dfrac{3^2}{3}=3\)
\(\Rightarrow\dfrac{9}{3+ab+bc+ac}\ge\dfrac{9}{3+3}=\dfrac{9}{6}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi: \(a=b=c=1\)



\(\Leftrightarrow ab^2+bc^2+ca^2\ge a^2b+b^2c+c^2a\)
\(\Leftrightarrow\left(c^2b-abc-b^2c+ab^2\right)+\left(ca^2+abc-ac^2-a^2b\right)\ge0\)
\(\Leftrightarrow b\left(c^2-ac-bc+ab\right)-a\left(c^2-ac-bc+ab\right)\ge0\)
\(\Leftrightarrow\left(b-a\right)\left(c^2-ac-bc+ab\right)\ge0\)
\(\Leftrightarrow\left(b-a\right)\left(c-b\right)\left(c-a\right)\ge0\) (luôn đúng do \(c\ge b\ge a>0\))