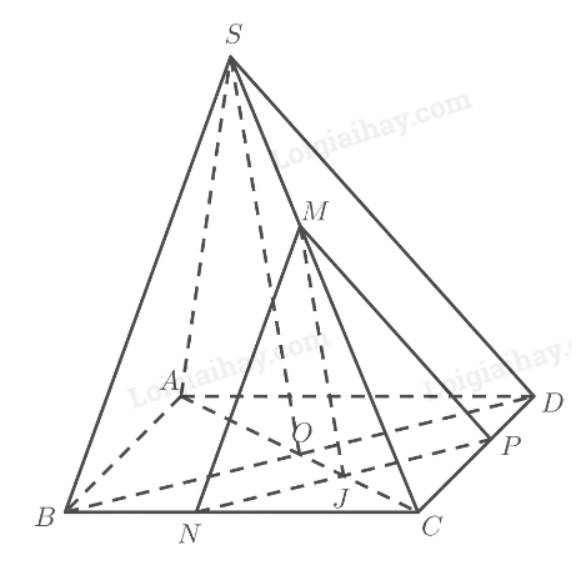
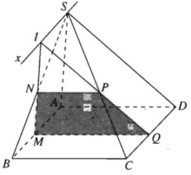
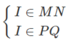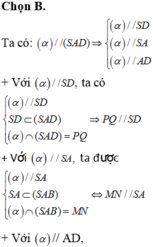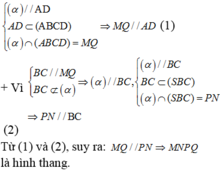Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên đoạn AB. Một mặt phẳng \(\left(\alpha\right)\) cắt SB, SC và CD lần lượt tại N, P và Q
a) Tứ giác MNPQ là hình gì ?
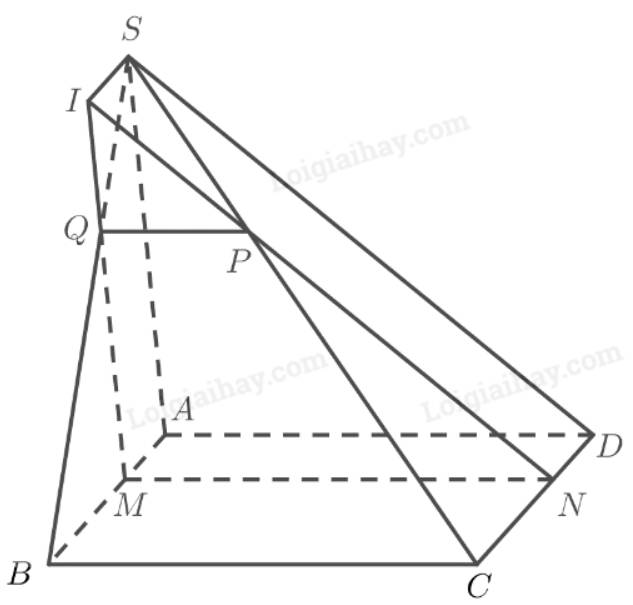
b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định ?



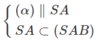 nên (α) ∩ (SAB) = MN
nên (α) ∩ (SAB) = MN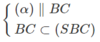 nên (α) ∩ (SBC) = NP
nên (α) ∩ (SBC) = NP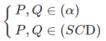 ⇒ (α) ∩ (SCD) = PQ
⇒ (α) ∩ (SCD) = PQ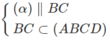 nên (α) ∩ (ABCD) = QM
nên (α) ∩ (ABCD) = QM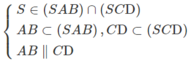 ⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD