NT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dưới đây là một vài câu hỏi có thể liên quan tới câu hỏi mà bạn gửi lên. Có thể trong đó có câu trả lời mà bạn cần!
NH
3
NT
29 tháng 12 2017
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\\ \Rightarrow\left\{{}\begin{matrix}1+\dfrac{x}{y}+\dfrac{x}{z}=0\\\dfrac{y}{x}+1+\dfrac{y}{z}=0\\\dfrac{z}{x}+\dfrac{z}{y}+1=0\end{matrix}\right.\\ \Rightarrow\dfrac{x}{y}+\dfrac{x}{z}+\dfrac{y}{x}+\dfrac{y}{z}+\dfrac{z}{x}+\dfrac{z}{y}=-3\)
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\\ \Rightarrow\dfrac{yz+xz+xy}{xyz}=0\\ \Rightarrow yz+xz+xy=0\)
\(\Rightarrow\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}\right)\left(xy+xz+yz\right)=0\\ \Rightarrow\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}+\dfrac{x}{y}+\dfrac{x}{z}+\dfrac{y}{x}+\dfrac{y}{z}+\dfrac{z}{x}+\dfrac{z}{y}=0\\ \Rightarrow\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}=3\)
ND
13 tháng 12 2017
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\)
\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{-1}{z}\)
\(\Rightarrow\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^3=\left(\dfrac{-1}{z}\right)^3\)
\(\Leftrightarrow\dfrac{1}{x^3}+3\dfrac{1}{x^2}\dfrac{1}{y}+3\dfrac{1}{x}\dfrac{1}{y^2}+\dfrac{1}{y^3}=\dfrac{-1}{z^3}\)
\(\Leftrightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=-3.\dfrac{1}{x}\dfrac{1}{y}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\)
\(\Leftrightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=-3\dfrac{1}{x}\dfrac{1}{y}\dfrac{-1}{z}\)
\(\Leftrightarrow\left(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}\right)xyz=3\dfrac{1}{x}\dfrac{1}{y}\dfrac{1}{z}.xyz\)
\(\Leftrightarrow\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}=3\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(M=\dfrac{\dfrac{1}{16}}{x^2}+\dfrac{\dfrac{1}{4}}{y^2}+\dfrac{1}{z^2}\ge\dfrac{\left(\dfrac{1}{4}+\dfrac{1}{2}+1\right)^2}{x^2+y^2+z^2}=\dfrac{49}{16}\)
\(M_{min}=\dfrac{49}{16}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{\sqrt{7}};\dfrac{2}{\sqrt{14}};\dfrac{2}{\sqrt{7}}\right)\)
ND
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
\(M=\dfrac{\dfrac{1}{16}}{x^2}+\dfrac{\dfrac{1}{4}}{y^2}+\dfrac{1}{z^2}\ge\dfrac{\left(\dfrac{1}{4}+\dfrac{1}{2}+1\right)^2}{x^2+y^2+z^2}=\dfrac{7}{4}\)
\(M_{min}=\dfrac{7}{4}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{1}{\sqrt{2}};1\right)\)
8 tháng 8 2017
a)(x-y)3+(y-z)3+(z-x)3
=3(x-y+y-z+z-x)=3
b)nhân vào là rồi đối trừ là hết luôn ( nhưng là mũ 2 hay nhân 2 v mk là theo nhân 2 nhé]
4 tháng 9 2021
a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)
AH
Akai Haruma
Giáo viên
22 tháng 9 2021
Lời giải:
Đặt $\frac{a}{x}=\frac{b}{y}=\frac{c}{z}=t$
$\Rightarrow a=xt; b=yt; c=zt$. Ta có:
$a+b+c=xt+yt+zt=t(x+y+z)=t$
$a^2+b^2+c^2=t^2(x^2+y^2+z^2)=t^2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{t^2-t^2}{2}=0$
Ta có đpcm.
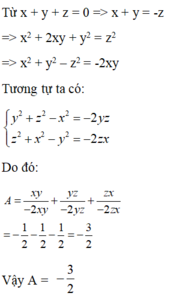
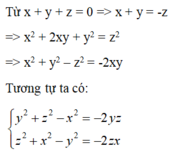
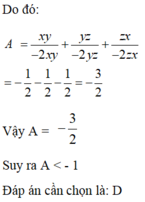
\(A=\left(x^2-yz\right)\left(y^2-zx\right)\left(z^2-xy\right)=\sqrt{\left(x^2-yz\right)\left(y^2-zx\right)}.\sqrt{\left(y^2-zx\right)\left(z^2-xy\right)}.\sqrt{\left(z^2-xy\right)\left(x^2-yz\right)}\)Giả sử \(x^2\ge yz;y^2\ge zx;z^2\ge xy\)
Theo Cosi ta có :
\(\sqrt{\left(x^2-yz\right)\left(y^2-zx\right)}\le\frac{x^2-yz+y^2-zx}{2}\)
\(\sqrt{\left(y^2-zx\right)\left(z^2-xy\right)}\le\frac{y^2-zx+z^2-xy}{2}\)
\(\sqrt{\left(z^2-xy\right)\left(x^2-yz\right)}\le\frac{z^2-xy+x^2-yz}{2}\)
Cộng theo vế ta được :
\(A\le\frac{x^2-yz+y^2-zx+y^2-zx+z^2-xy+z^2-xy+x^2-yz}{2}=\left(x^2+y^2+z^2\right)-\left(xy+yz+zx\right)\)
\(=1-\left(xy+yz+zx\right)\le1-\left(x^2+y^2+z^2\right)=1-1=0\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y=z=\frac{1}{3}\) hoặc \(x=y=z=\frac{-1}{3}\) ( thỏa mãn giả sử )
Chúc bạn học tốt ~
PS : ko chắc :v
Em vừa giải bên AoPS: