Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
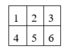
+ Tô màu ô vuông số 2: có C 3 2 cách chọn 2 trong 3 màu, có C 4 2 cách tô 2 màu đó lên 4 cạnh. Vậy có C 3 2 C 4 2 = 18cách.
+ Tô màu ô vuông số 1,5,3: có C 2 1 cách chọn màu còn lại, có C 3 2 cách tô màu còn lại lên 3 cạnh còn lại của 1 hình vuông. Vậy có ( C 2 1 C 3 2 ) 3 = 6 3 cách
+ Tô màu ô vuông số 4,6: Mỗi 1 hình vuông có 2 cách tô màu. Vậy có 2 2 = 4cách.
Vậy có 18. 6 3 .4 = 15552 cách thỏa mãn.
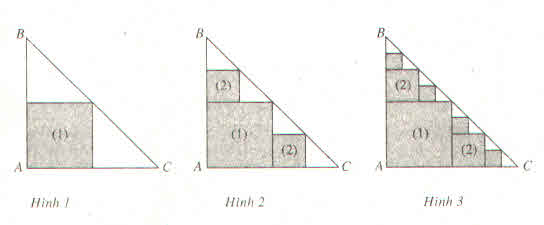
a) Gọi \({u_n}\) là độ dài cạnh của hình vuông thứ \(n\).
Ta có: \({u_1} = 1;{u_2} = \frac{{{u_1}}}{2}.\sqrt 2 = \frac{{{u_1}}}{{\sqrt 2 }};{u_3} = \frac{{{u_2}}}{2}.\sqrt 2 = \frac{{{u_2}}}{{\sqrt 2 }};...\)
Từ đó ta thấy \(\left( {{u_n}} \right)\) là một cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \({u_n} = {u_1}.{q^{n - 1}} = 1.{\left( {\frac{1}{{\sqrt 2 }}} \right)^{n - 1}} = \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Diện tích của hình vuông thứ \(n\) là: \({a_n} = u_n^2 = {\left( {\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)^2} = \frac{1}{{{2^{n - 1}}}},n = 1,2,3,...\)
Vậy \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}}\)
Đây là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\).
Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = 2\left( {1 - \frac{1}{{{2^n}}}} \right)\).
\(\lim {S_n} = \lim 2\left( {1 - \frac{1}{{{2^n}}}} \right) = 2\left( {1 - \lim \frac{1}{{{2^n}}}} \right) = 2\left( {1 - 0} \right) = 2\).
b) Chu vi của hình vuông thứ \(n\) là: \({p_n} = 4{u_n} = 4.\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}},n = 1,2,3,...\)
Vậy \({Q_n} = 4 + \frac{4}{{\sqrt 2 }} + \frac{4}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 4\left( {1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}} \right)\)
\(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}}\) là tổng của cấp số nhân có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{{\sqrt 2 }}\).
Vậy \(1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + ... + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n - 1}}}} = 1.\frac{{1 - {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^n}}}{{1 - \frac{1}{{\sqrt 2 }}}} = \left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\).
\( \Rightarrow {Q_n} = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\)
\(\begin{array}{l}\lim {Q_n} = \lim 4\left( {2 + \sqrt 2 } \right)\left( {1 - \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right) = 4\left( {2 + \sqrt 2 } \right)\left( {1 - \lim \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\\ & = 4\left( {2 + \sqrt 2 } \right)\left( {1 - 0} \right) = 4\left( {2 + \sqrt 2 } \right)\end{array}\).
Chọn C
Đa giác đều có 20 cạnh thì sẽ có tất cả 10 đường chéo đi qua tâm của đa giác.
Một hình chữ nhật được tạo thành từ 2 đường chéo đi qua tâm, suy ra số hình chữ nhật được tạo thành là C 10 2
Hình vuông được tạo thành từ 2 đường chéo vuông góc nhau, ta có tất cả 5 cặp đường chéo vuông góc nhau, suy ra có tất cả 5 hình vuông.
Vậy có 40 hình chữ nhật (không phải hình vuông) được tạo thành.
a) \({S_n} = {5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2} = {5^n}.\frac{1}{{{9^n}}} = {\left( {\frac{5}{9}} \right)^n},n = 1,2,3,...\)
\(\lim {S_n} = \lim {\left( {\frac{5}{9}} \right)^n} = 0\)
b) \({p_n} = {5^n}.4.\frac{1}{{{3^n}}} = 4.{\left( {\frac{5}{3}} \right)^n},n = 1,2,3,...\)
\(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right)\)
Vì \(\lim \frac{1}{{4.{{\left( {\frac{5}{3}} \right)}^n}}} = \frac{1}{4}.\lim {\left( {\frac{3}{5}} \right)^n} = 0\) và \(4.{\left( {\frac{5}{3}} \right)^n} > 0\) với mọi \(n\) nên \(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right) = + \infty \).
a) Ta có: \({u_1} = {1^2};{u_2} = {2^2};{u_3} = {3^2};...;{u_n} = {n^2}\)
\(\begin{array}{l}{u_n} > 10000 \Leftrightarrow {n^2} > 10000 = {100^2} \Leftrightarrow n > 100\\{u_n} > 1000000 \Leftrightarrow {n^2} > 1000000 = {1000^2} \Leftrightarrow n > 1000\end{array}\)
b) \({u_n} > S \Leftrightarrow {n^2} > S \Leftrightarrow n > \sqrt S \).
Vậy với các số tự nhiên \(n > \sqrt S \) thì \({u_n} > S\).
Đáp án A
Số tam giác tạo bởi các đỉnh của đa giác là C 7 3 =35
Số tam giác có 2 cạnh là 2 cạnh của đa giác là 7
Số tam giác có 1 cạnh là cạnh của đa giác là 
Vậy số tam giác tạo bởi đỉnh của đa giác và không có cạnh trùng với cạnh của đa giác là 
tam giác.
Cạnh của hình vuông C1 là: a1 = 4 (giả thiết)
Giả sử cạnh hình vuông thứ n là an.
Theo định lý Py-ta-go : Cạnh hình vuông thứ n + 1 là :
⇒ (an) là cấp số nhân với a1 = 4 và công bội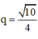 
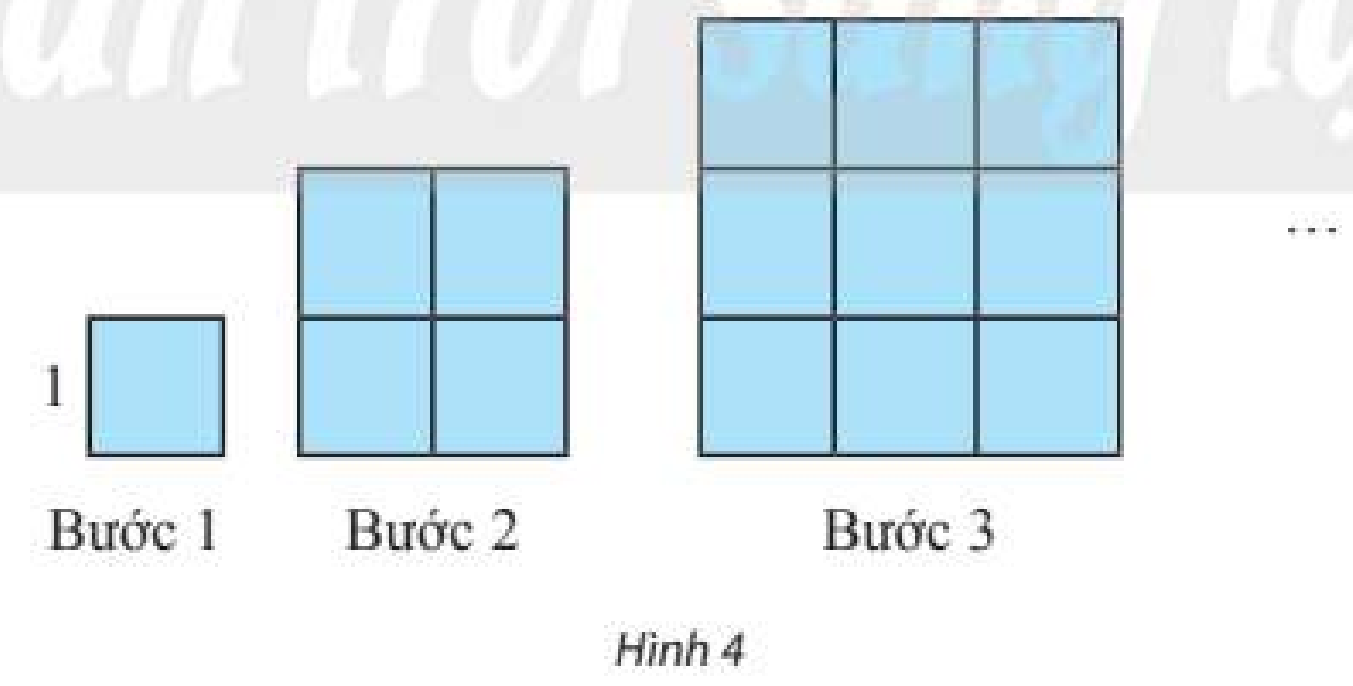
Diện tích ô vuông màu xanh sau lần phân chia thứ nhất là \(\frac{1}{9}\), số ô vuông màu xanh được tạo thêm là \({8^0}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ hai là \(\frac{1}{{{9^2}}}\), số ô vuông màu xanh được tạo thêm là \({8^1}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ ba là \(\frac{1}{{{9^3}}}\), số ô vuông màu xanh được tạo thêm là \({8^2}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ tư là \(\frac{1}{{{9^4}}}\), số ô vuông màu xanh được tạo thêm là \({8^3}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ ba là \(\frac{1}{{{9^5}}}\), số ô vuông màu xanh được tạo thêm là \({8^4}\).
Tổng diện tích các ô vuông màu xanh là
\(\frac{1}{9} + \frac{1}{{{9^2}}} \times {8^1} + \frac{1}{{{9^3}}} \times {8^2} + \frac{1}{{{9^4}}} \times {8^3} + \frac{1}{{{9^5}}} \times {8^4} = 0,445\).
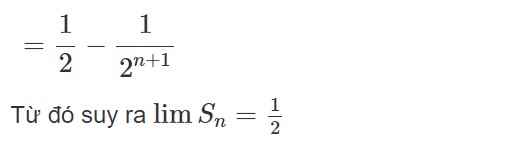
Chọn B
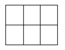
Số cách chọn ra 3 đỉnh trong số 25 đỉnh của các hình vuông đơn vị là: C 25 3
TH1: 3 đỉnh nằm trên cùng 1 hàng hoặc cùng 1 cột là: 5 C 5 3 + 5 C 5 3
TH2: 3 đỉnh nằm trên một trong các đường chéo của hình vuông kích thước 4x4, 3x3, 2x2 sao cho các đường chéo ấy không trùng nhau là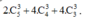
TH3: 3 đỉnh nằm trên một trong các đường chéo của hình chữ nhật kích thước 2x4. Số hình chữ nhật đó là 6. Do đó số cách chọn là 12
Vậy số tam giác được tạo thành là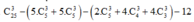
= 2148