Cho 3 số thực a, b, c thỏa mãn \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
Chứng minh \(\frac{a}{\left(b-c\right)^2}+\frac{b}{\left(c-a\right)^2}+\frac{c}{\left(a-b\right)^2}=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
28 tháng 8 2020
Áp dụng giả thiết và một đánh giá quen thuộc, ta được: \(16\left(a+b+c\right)\ge\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{ab+bc+ca}{abc}=\frac{\left(ab+bc+ca\right)^2}{abc\left(ab+bc+ca\right)}\ge\frac{3\left(a+b+c\right)}{ab+bc+ca}\)hay \(\frac{1}{6\left(ab+bc+ca\right)}\le\frac{8}{9}\)
Đến đây, ta cần chứng minh \(\frac{1}{\left(a+b+\sqrt{2\left(a+c\right)}\right)^3}+\frac{1}{\left(b+c+\sqrt{2\left(b+a\right)}\right)^3}+\frac{1}{\left(c+a+\sqrt{2\left(c+b\right)}\right)^3}\le\frac{1}{6\left(ab+bc+ca\right)}\)
Áp dụng bất đẳng thức Cauchy cho ba số dương ta có \(a+b+\sqrt{2\left(a+c\right)}=a+b+\sqrt{\frac{a+c}{2}}+\sqrt{\frac{a+c}{2}}\ge3\sqrt[3]{\frac{\left(a+b\right)\left(a+c\right)}{2}}\)hay \(\left(a+b+\sqrt{2\left(a+c\right)}\right)^3\ge\frac{27\left(a+b\right)\left(a+c\right)}{2}\Leftrightarrow\frac{1}{\left(a+b+2\sqrt{a+c}\right)^3}\le\frac{2}{27\left(a+b\right)\left(a+c\right)}\)
Hoàn toàn tương tự ta có \(\frac{1}{\left(b+c+2\sqrt{b+a}\right)^3}\le\frac{2}{27\left(b+c\right)\left(b+a\right)}\); \(\frac{1}{\left(c+a+2\sqrt{c+b}\right)^3}\le\frac{2}{27\left(c+a\right)\left(c+b\right)}\)
Cộng theo vế các bất đẳng thức trên ta được \(\frac{1}{\left(a+b+\sqrt{2\left(a+c\right)}\right)^3}+\frac{1}{\left(b+c+\sqrt{2\left(b+a\right)}\right)^3}+\frac{1}{\left(c+a+\sqrt{2\left(c+b\right)}\right)^3}\le\frac{4\left(a+b+c\right)}{27\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)Phép chứng minh sẽ hoàn tất nếu ta chỉ ra được \(\frac{4\left(a+b+c\right)}{27\left(a+b\right)\left(b+c\right)\left(c+a\right)}\le\frac{1}{6\left(ab+bc+ca\right)}\)\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge\frac{8}{9}\left(ab+bc+ca\right)\left(a+b+c\right)\)
Đây là một đánh giá đúng, thật vậy: đặt a + b + c = p; ab + bc + ca = q; abc = r thì bất đẳng thức trên trở thành \(pq-r\ge\frac{8}{9}pq\Leftrightarrow\frac{1}{9}pq\ge r\)*đúng vì \(a+b+c\ge3\sqrt[3]{abc}\); \(ab+bc+ca\ge3\sqrt[3]{\left(abc\right)^2}\))
Vậy bất đẳng thức được chứng minh
Đẳng thức xảy ra khi \(a=b=c=\frac{1}{4}\)
BT
8 tháng 4 2018
Ta có \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{1}{a+b+c}=0\)
\(\Leftrightarrow\left(\frac{1}{a}-\frac{1}{a+b+c}\right)+\left(\frac{1}{b}+\frac{1}{c}\right)=0\)
\(\Leftrightarrow\frac{b+c}{a\left(a+b+c\right)}+\frac{b+c}{bc}=0\)
\(\Leftrightarrow\left(b+c\right)\left(\frac{1}{a\left(a+b+c\right)}+\frac{1}{bc}\right)=0\)
\(\Leftrightarrow\left(b+c\right)\frac{bc+a^2+ab+ac}{abc\left(a+b+c\right)}=0\)
\(\Leftrightarrow\left(b+c\right)\frac{\left(a+b\right)\left(c+a\right)}{abc\left(a+b+c\right)}=0\)
=> b+c=0 hoặc a+b=0 hoặc c+a=0
Đến đây bn => a=-b;b=-c;c=-a lần lượt thay vào VT là xog
19 tháng 2 2022
Từ bất đẳng thức Cô si ta có:
\(4\left(ab+bc+ca\right)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\le\left[\frac{ab+bc+ca}{ca}+ca\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\right]^2\)
\(\Rightarrow\)Ta cần chứng minh:
\(\frac{ab+bc+ca}{ca}+ca\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\le\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}\)
Vì vai trò của a, b, c trong bất đẳng thức như nhau, nên không mất tính tổng quát ta giả sử \(a\ge b\ge c\)nên bất đẳng thức cuối cùng đùng. Vậy bất đẳng thức được chứng minh.
TN
23 tháng 8 2017
Bài này làm hoài :v
Áp dụng BĐT Cauchy-Schwarz và BĐT AM-GM ta có:
\(VT=\frac{b^2c^2}{ab+ac}+\frac{a^2c^2}{ab+bc}+\frac{a^2b^2}{ac+bc}\)
\(\ge\frac{\left(ab+bc+ca\right)^2}{2\left(ab+bc+ca\right)}=\frac{ab+bc+ca}{2}\)
\(\ge\frac{3\sqrt[3]{\left(abc\right)^2}}{2}=\frac{3}{2}=VP\)
Khi a=b=c=1
PN
2 tháng 9 2020
Đặt \(\left\{a;b;c\right\}\rightarrow\left\{\frac{1}{x};\frac{1}{y};\frac{1}{z}\right\}\)Khi đó : \(\frac{1}{x}.\frac{1}{y}.\frac{1}{z}=\frac{1}{x.y.z}=a.b.c=1< =>x.y.z=1\)
\(BĐT< =>\frac{1}{\left(\frac{1}{x}\right)^3\left(\frac{1}{y}+\frac{1}{z}\right)}+\frac{1}{\left(\frac{1}{y}\right)^3\left(\frac{1}{y}+\frac{1}{x}\right)}+\frac{1}{\left(\frac{1}{z}\right)^3\left(\frac{1}{x}+\frac{1}{y}\right)}\ge\frac{3}{2}\)
\(< =>\frac{x^3yz}{y+z}+\frac{y^3xz}{z+x}+\frac{z^3xy}{x+y}\ge\frac{3}{2}\)\(< =>\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\ge\frac{3}{2}\)(*)
Ta chỉ cần chỉ ra bất đẳng thức (*) đúng thì bài toán được giải quyết , thật vậy :
Theo bất đẳng thức Bunhiacopxki dạng phân thức :
\(\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y}\ge\frac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\frac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\frac{x+y+z}{2}\) (**)
Sử dụng bất đẳng thức AM-GM ta có :
\(x+y+z\ge3\sqrt[3]{xyz}=3\sqrt[3]{1}=3\)Tương đương \(\frac{x+y+z}{2}\ge\frac{3}{2}\)(***)
Từ (**) và (***) ta được \(\frac{x^2}{z+y}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\ge\frac{x+y+z}{2}\ge\frac{3}{2}\)
Suy ra bất đẳng thức (*) đúng . Nên ta có điều phải chứng minh !
Dấu "=" xảy ra khi và chỉ khi \(x=y=z=1< =>a=b=c=1\)
31 tháng 3 2021
(
hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
hhhhhhhhhhhhhhhhh
hhhhhhhhhhhhhhhhhh
hhhhhhhhhhhhhhh
hhhhhhhhhhhhh
VD
27 tháng 4 2020
\(=\)\(18\left(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}\right)\)\(=\)\(18\frac{3}{1}\)\(>\)\(\left(9+5\sqrt{3}\right)\left(a^2+b^2+c^2\right)\)\(=\)\(0\)
Vậy\(18\frac{3}{1}\)\(>\)\(0\)
Chứng minh là \(18\frac{3}{1}\)\(>\)\(0\)là đúng
chúc bạn học tốt
A
27 tháng 4 2020
Bất đẳng thức trên
<=> 
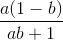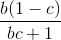+ 1 + 
+ 1 +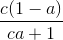 
+ 1 ≥ 3
<=> 
+ 
+ 
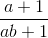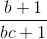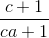≥ 3 (*)
Ta có: VT(*) ≥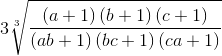 
Ta sẽ chứng minh: (a + 1)(b + 1)(c + 1) ≥ (ab + 1)(bc + 1)(ca + 1)
<=> abc + ab + bc + ca + a + b + c + 1
≥ a2b2c2 + abc(a + b + c) + ab + bc + ca + 1
<=> 3 ≥ a2b2c2 + 2abc (**)
Theo Cosi: 3 = a + b + c ≥ 3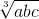
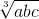=> ≤ 1 => abc ≤ 1
Vậy (**) đúng => (*) đúng.
20 tháng 6 2020
\(\frac{1}{\left(1+a\right)^2}+\frac{1}{\left(1+b\right)^2}+\frac{1}{\left(1+b\right)^2}+\frac{2}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}\ge1\)
<=> \(\left(1+b\right)^2\left(1+c\right)^2+\left(1+a\right)^2\left(1+b\right)^2+\left(1+a\right)\left(1+c\right)^2\)
\(+2\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge\left(1+a\right)^2\left(1+b\right)^2\left(1+c\right)^2\)
<=> \(a^2+b^2+c^2\ge3\)đúng vì \(a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}=3\)
Dấu "=" xảy ra <=> a = b = c = 1
gia thiet la = chu nhi, sao lai +.neu la bag thi ban nhan cheo roi phan h thanh nhan tu.(a+b)(c+b)(c+a)=0 thay vao la ra