Nếu a và b là 2 số nguyên dương thỏa mãn a2 - b2 = 97. Gía trị của biểu thức a2 + b2 là bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LA
21 tháng 4 2021
Để \(\frac{2a+2b}{ab+1}\) là bình phương của 1 số nguyên thì 2a + 2b chia hết cho ab + 1; mà ab + 1 chia hết cho 2a + 2b => ab + 1 = 2b + 2a
=> \(\frac{2a+2b}{ab+1}\)=1 = 12
CM
9 tháng 12 2018
Đáp án D
Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất
CM
23 tháng 5 2017
Ta có:
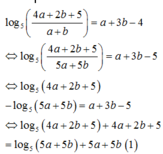
Xét hàm số
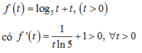
Hàm số f t đồng biến trên 0 ; + ∞
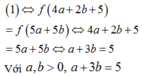
ta có:
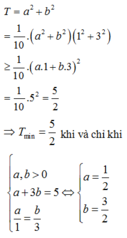
Chọn: D
CM
20 tháng 10 2017
Đáp án B
Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4
⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b
Xét hàm số f t = log 5 t + t t > 0 ⇒ f t đồng biến trên 0 ; + ∞
Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b
⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2
TD
1
AH
Akai Haruma
Giáo viên
30 tháng 11 2021
Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ bên trái khung soạn thảo) để được hỗ trợ tốt hơn.
CM
15 tháng 9 2019
Vì: a + 1 1 + b 2 = a + 1 − b 2 ( a + 1 ) 1 + b 2 ; 1 + b 2 ≥ 2 b n ê n a + 1 1 + b 2 ≥ a + 1 − b 2 ( a + 1 ) 2 b = a + 1 − a b + b 2
Tương tự: b + 1 1 + c 2 ≥ b + 1 − b c + c 2 ; c + 1 1 + a 2 ≥ c + 1 − c a + a 2 ⇒ M ≥ a + b + c + 3 − ( a + b + c ) + ( a b + b c + c a ) 2 = 3 + 3 − ( a b + b c + c a ) 2
Chứng minh được: 3 ( a b + b c + c a ) ≤ ( a + b + c ) 2 = 9 a c ⇒ 3 − ( a b + b c + c a ) 2 ≥ 0 ⇒ M ≥ 3
Dấu “=” xảy ra khi a = b = c = 1. Giá trị nhỏ nhất của M bằng 3.
NN
2
DT
Dang Tung
CTVHS
12 tháng 6 2023
Sửa đề : \(\dfrac{a^2}{a^2+b}+\dfrac{b^2}{b^2+a}\le1\\ \) (*)
\(< =>\dfrac{a^2\left(b^2+a\right)+b^2\left(a^2+b\right)}{\left(a^2+b\right)\left(b^2+a\right)}\le1\\ < =>a^2b^2+a^3+b^2a^2+b^3\le\left(a^2+b\right)\left(b^2+a\right)\) ( Nhân cả 2 vế cho `(a^{2}+b)(b^{2}+a)>0` )
\(< =>a^3+b^3+2a^2b^2\le a^2b^2+b^3+a^3+ab\\ < =>a^2b^2\le ab\\ < =>ab\le1\) ( Chia 2 vế cho `ab>0` )
Do a,b >0
Nên áp dụng BDT Cô Si :
\(2\ge a+b\ge2\sqrt{ab}< =>\sqrt{ab}\le1\\ < =>ab\le1\)
Do đó (*) luôn đúng
Vậy ta chứng minh đc bài toán
Dấu "=" xảy ra khi : \(a=b>0,a+b=2< =>a=b=1\)
LD
22 tháng 7 2023
a Sửa đề : Chứng minh \(\dfrac{a^2}{a^2+b}\)+\(\dfrac{b^2}{b^2+a}\)\(\le\) 1 ( Đề thi vào 10 Hà Nội).
Bất đẳng thức trên tương đương :
\(\dfrac{a^2+b-b}{a^2+b}\)+\(\dfrac{b^2+a-a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\) 1 - \(\dfrac{b}{a^2+b}\)+ 1 - \(\dfrac{a}{b^2+a}\)\(\le\)1
\(\Leftrightarrow\)1 - \(\dfrac{b}{a^2+b}\) - \(\dfrac{a}{b^2+a}\)\(\le\)0
\(\Leftrightarrow\)- \(\dfrac{b}{a^2+b}\)- \(\dfrac{a}{b^2+a}\)\(\le\)-1
\(\Leftrightarrow\)\(\dfrac{a}{b^2+a}\)+ \(\dfrac{b}{a^2+b}\)\(\ge\)1
Xét VT = \(\dfrac{a^2}{ab^2+a^2}\)+ \(\dfrac{b^2}{a^2b+b^2}\)\(\ge\)\(\dfrac{\left(a+b\right)^2}{ab^2+a^2+a^2b+b^2}\) (Cauchy - Schwarz)
= \(\dfrac{\left(a+b\right)^2}{ab\left(b+a\right)+a^2+b^2}\)
\(\ge\)\(\dfrac{\left(a+b\right)^2}{2ab+a^2+b^2}\)
= \(\dfrac{\left(a+b\right)^2}{\left(a+b\right)^2}\)= 1
Vậy BĐT được chứng minh
Dấu '=' xảy ra \(\Leftrightarrow\)a = b = 1
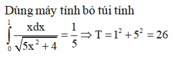
Kết quả =4705
ta có a^2-b^2=97 =>(a-b)(a+b)=97
Vì a,b dương và a-b<a+b nên =>a-b=1,a+b=97 (ước của 97 là 1 và 97)
có tổng và hiệu ta tính đc a=49,b=48
=>a^2+b^2=49^2+48^2=4705