Cho k là một số tự nhiên. Chứng minh rằng:
\(C_5^0.C_{2011}^k+C_5^1.C_{2011}^{k-1}+...+C_5^5.C_{2011}^{k-5}=C_{2016}^k\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Để tính \(A_{15}^{10}\) ta ấn liên tiếp các phím
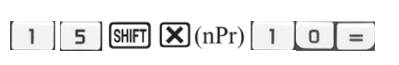
Thì nhận được kết quả là \(1,{08972864.10^{10}}\)
b) Để tính \(C_{10}^6 + C_{10}^7 + C_{11}^8\) thì ta ấn liên tiếp các phím
Thì ta nhận được kết quả là 495
c) Để tính \(C_5^1C_{20}^2 + C_5^2C_{20}^1\) thì ta ấn liên tiếp các phím
Thì ta được kết quả là 1150
HN
22 tháng 11 2017
1/ \(2C^k_n+5C^{k+1}_n+4C^{k+2}_n+C^{k+3}_n\)
\(=2\left(C^k_n+C_n^{k+1}\right)+3\left(C^{k+1}_n+C^{k+2}_n\right)+\left(C^{k+2}_n+C^{k+3}_n\right)\)
\(=2C_{n+1}^{k+1}+3C_{n+1}^{k+2}+C_{n+1}^{k+3}\)
\(=2\left(C_{n+1}^{k+1}+C_{n+1}^{k+2}\right)+\left(C_{n+1}^{k+2}+C^{k+3}_{n+1}\right)\)
\(=2C_{n+2}^{k+2}+C_{n+2}^{k+3}=C_{n+2}^{k+2}+\left(C_{n+2}^{k+2}+C_{n+2}^{k+3}\right)=C_{n+2}^{k+2}+C_{n+3}^{k+3}\)
28 tháng 11 2017
Áp dụng ct:C(k)(n)=C(k)(n-1)+C(k-1)(n-1) có:
................C(k-1)(n-1)= C(k)(n) - C(k)(n-1)
tương tự: C(k-1)(n-2)= C(k)(n-1) - C(k)(n-2)
................C(k-1)(n-3)= C(k)(n-2) -C(k)(n-3)
.........................................
................C(k-1)(k-1)= C(k)(k) (=1)
Cộng 2 vế vào với nhau...-> đpcm
HP
12 tháng 8 2021
\(C_{14}^k+C_{14}^{k+2}=2C_{14}^{k+1}\)
\(\Leftrightarrow\dfrac{14!}{\left(14-k\right)!k!}+\dfrac{14!}{\left(12-k\right)!\left(k+2\right)!}=\dfrac{2.14!}{\left(13-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\dfrac{14!}{k!\left(12-k\right)!}\left[\dfrac{1}{\left(14-k\right)\left(13-k\right)}+\dfrac{1}{\left(k+1\right)\left(k+2\right)}\right]=\dfrac{2}{\left(13-k\right)\left(k+1\right)}.\dfrac{14!}{k!\left(12-k\right)!}\)
\(\Leftrightarrow\dfrac{2k^2-24k+184}{\left(14-k\right)\left(k+2\right)\left(13-k\right)\left(k+1\right)}=\dfrac{2}{\left(13-k\right)\left(k+1\right)}\)
\(\Leftrightarrow\dfrac{k^2-12k+92}{-k^2+12k+28}=1\)
\(\Leftrightarrow k^2-12k+92=-k^2+12k+28\)
\(\Leftrightarrow k^2-12k+32=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=4\\k=8\end{matrix}\right.\)
QT
1
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
\(\begin{array}{l}C_5^0 - C_5^1 + C_5^2 - C_5^3 + C_5^4 - C_5^5\\ = C_5^0{.1^5} - C_5^1{.1^4}.1 + C_5^2{.1^3}{.1^2} - C_5^3{.1^2}{.1^3} + C_5^4{.1.1^4} - C_5^5{.1^5}\\ = {\left( {1 - 1} \right)^5} = {0^5}\\ = 0\end{array}\)
Vậy ta có điều phải chứng minh
Cách 2:
Ta có: \(C_5^0 = C_5^{5 - 0} = C_5^5\)
Tương tự: \(C_5^1 = C_5^{5 - 1} = C_5^4;\;C_5^2 = C_5^{5 - 2} = C_5^3;\)
\(\Rightarrow C_5^0 - C_5^1 + C_5^2 - C_5^3 + C_5^4 - C_5^5 = \left( {C_5^0 - C_5^5} \right) + \left( {C_5^4 - C_5^1} \right) + \left( {C_5^2 - C_5^3} \right) = 0\) (đpcm)
thành một đa thức có {\displaystyle n+1}
số hạng:
(1) với mọi số tự nhiên n.
và {\displaystyle \sum _{k=0}^{n}C_{n}^{k}x^{k+1}=\sum _{k=1}^{n}C_{n}^{k-1}x^{k}+x^{n+1}}
và do đó {\displaystyle (a+b)^{n}=a^{n}(1+{\frac {b}{a}})^{n}=a^{n}\sum _{k=0}^{n}C_{n}^{k}{\frac {b^{k}}{a^{k}}}=\sum _{k=0}^{n}C_{n}^{k}a^{n-k}b^{k}}
:
^{4}&=x^{4}+4x^{3}y+6x^{2}y^{2}+4xy^{3}+y^{4},\\[8pt](x+y)^{5}&=x^{5}+5x^{4}y+10x^{3}y^{2}+10x^{2}y^{3}+5xy^{4}+y^{5},\\[8pt](x+y)^{6}&=x^{6}+6x^{5}y+15x^{4}y^{2}+20x^{3}y^{3}+15x^{2}y^{4}+6xy^{5}+y^{6},\\[8pt](x+y)^{7}&=x^{7}+7x^{6}y+21x^{5}y^{2}+35x^{4}y^{3}+35x^{3}y^{4}+21x^{2}y^{5}+7xy^{6}+y^{7}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e30228a99653e6b9a65ae6640a3b7f85e2fdf144)
giảm dần cho tới khi đạt đến 0 ({\displaystyle x^{0}=1}
), giá trị bắt đầu là {\displaystyle n}
.)
tăng lên bắt đầu từ 0 ({\displaystyle y^{0}=1}
) cho tới khi đạt đến {\displaystyle n}
.
là một số thực và {\displaystyle z}
là một số phức có module nhỏ hơn 1 thì:
18 tháng 5 2017
Ta có :
\(C^{k+1}_{n+1}=C^k_n+C_n^{k+1}\)
\(C^{k+1}_n=C^k_{n-1}+C_{n-1}^{k+1}\)
...........
\(C^{k+1}_{k+2}=C^k_{k+1}+C_{k+1}^{k+1}\)
Từ đó :
\(C^{k+1}_{n+1}=C^k_n+C_{n-1}^k+....C^k_{k+1}+C^{k+1}_{k+1}\)
= \(C^k_n+C_{n-1}^k+....+C^k_{k+1}+C^k_k\)
Lời giải:
Theo nhị thức Newton:
$C^k_{2016}$ chính là hệ số của $x^k$ trong khai triển $(x+1)^{2016}(*)$
Lại có:
$(x+1)^{2016}=(x+1)^5.(x+1)^{2011}$
\(=(\sum \limits_{i=0}^5C^i_5x^i)(\sum \limits_{j=0}^{2011}C^i_{2011}x^j)\)
Hệ số $x^k$ trong khai triển này tương ứng với $0\leq i\leq 5; 0\leq j\leq 2011$ thỏa mãn $i+j=k$
Hay hệ số của $x^k$ trong khai triển $(x+1)^{2016}$ là:
$C^0_5.C^k_{2011}+C^1_5.C^{k-1}_{2011}+C^2_5C^{k-2}_{2011}+C^3_5.C^{k-3}_{2011}+C^4_5.C^{k-4}_{2011}+C^5_5.C^{k-5}_{2011}(**)$
Từ $(*); (**)$ ta có đpcm.