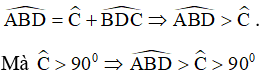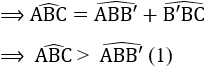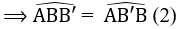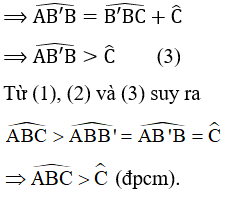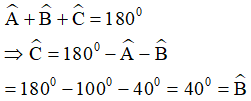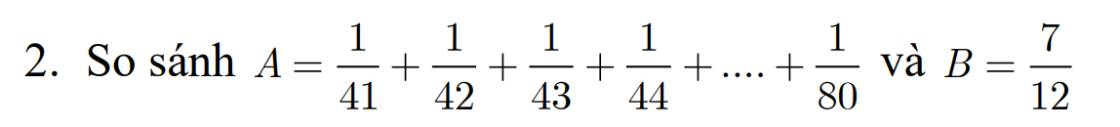có ai biết làm bài 7 câu b ko giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

Phải bảo quản thực phẩm để thực phẩm ko bị mất đi giá trị dinh dưỡng vốn có và giữ được sự tươi ngon, tránh bị biến chất khiến người ăn bị ngộ độc.
Bạn ơi, nếu mình lỡ có sai thì lên mạng tra nhé!

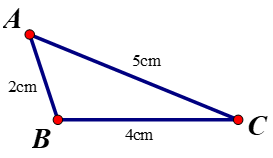
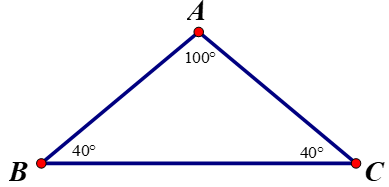
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
2)heo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Kiến thức áp dụng
+ Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Định lý tổng ba góc trong tam giác: Trong một tam giác, tổng ba góc bằng 180º.
3 a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
b) Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có
4) Trong một tam giác ta luôn có:
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn
⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.
+ Góc nhỏ nhất luôn là góc nhọn.
(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn
⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.
5) + Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.
6)Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
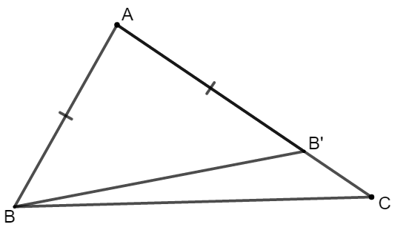
7)
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.
c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C


2. So sánh: A = \(\dfrac{1}{41}\) + \(\dfrac{1}{42}\) + \(\dfrac{1}{43}\) + \(\dfrac{1}{44}\)+...+ \(\dfrac{1}{80}\) và B = \(\dfrac{7}{12}\)
\(\dfrac{1}{41}>\dfrac{1}{42}>\dfrac{1}{43}>...>\dfrac{1}{60}\)
Xét mẫu số các phân số trên lần lượt là các số thuộc dãy số sau:
41; 42; 43;...;60
Dãy số trên là dãy số cách đều với khoảng cách là: 42 - 41 =1
Số số hạng của dãy số trên là: (60 - 41):1 + 1 = 20
⇒ \(\dfrac{1}{41}\) + \(\dfrac{1}{42}\)+...+ \(\dfrac{1}{60}\) > \(\dfrac{1}{60}\) \(\times\) 20 = \(\dfrac{1}{3}\) (1)
Chứng minh tương tự ta cũng có:
\(\dfrac{1}{61}+\dfrac{1}{62}+...+\dfrac{1}{80}\) > \(\dfrac{1}{80}\) \(\times\) 20 = \(\dfrac{1}{4}\) (2)
Kết hợp(1) và (2) ta có:
A = \(\dfrac{1}{41}+\dfrac{1}{42}+\dfrac{1}{43}+\dfrac{1}{44}+...+\dfrac{1}{80}\) > \(\dfrac{1}{3}\) + \(\dfrac{1}{4}\) = \(\dfrac{7}{12}\)
Vậy A > B