cho a,b,c là số thực dương, tìm Max: \(\sqrt{\dfrac{a}{b+c+2a}}+\sqrt{\dfrac{b}{c+a+2b}}+\sqrt{\dfrac{c}{a+b+2c}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PM
1 tháng 5 2018
ad bunhiacopxki ta có
A^2 \(\le3\left(\dfrac{a}{b+c+2a}+\dfrac{b}{c+a+2c}+\dfrac{c}{a+b+2c}\right)\)
Đặt B=\(\dfrac{a}{b+c+2a}+\dfrac{b}{c+a+2b}+\dfrac{c}{a+b+2c}\)
\(\Leftrightarrow\)B-3 =-\(\left(a+b+c\right)\) \(\left(\dfrac{1}{b+c+2a}+\dfrac{1}{c+a+2b}+\dfrac{1}{a+b+2a}\right)\)
dễ CM \(\dfrac{1}{a+b+2c}+\dfrac{1}{b+c+2a}+\dfrac{1}{c+a+2b}\)\(\ge\dfrac{9}{4\left(a+c+b\right)}\)
\(\Rightarrow\)B-3\(\le\)\(\dfrac{-9}{4}\)\(\Rightarrow\)B\(\le\dfrac{3}{4}\)
\(\Rightarrow A^2\le\dfrac{9}{4}\) mà A>0
\(\Rightarrow\)A\(\le\dfrac{3}{2}\)Dấu = xra khi a=b=c
NL
17 tháng 4 2018
Áp dụng liên tiếp Bunyakovsky và Cauchy-Schwarz ta được: \(NL^2=\left(\sqrt{\dfrac{a}{2a+b+c}}+\sqrt{\dfrac{b}{2b+a+c}}+\sqrt{\dfrac{c}{2c+a+b}}\right)^2\) \(\le\left(1^2+1^2+1^2\right)\left(\dfrac{a}{2a+b+c}+\dfrac{b}{2b+a+c}+\dfrac{c}{2c+a+b}\right)=3\left(\dfrac{a}{2a+b+c}+\dfrac{b}{2b+a+c}+\dfrac{c}{2c+a+b}\right)\) \(=3\left(\dfrac{a}{\left(a+b\right)+\left(a+c\right)}+\dfrac{b}{\left(a+b\right)+\left(b+c\right)}+\dfrac{c}{\left(a+c\right)+\left(b+c\right)}\right)\le\dfrac{3}{4}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}+\dfrac{b}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}+\dfrac{c}{b+c}\right)=\dfrac{3}{4}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{a+c}{a+c}\right)=\dfrac{3}{4}.3=\dfrac{9}{4}\)\(NL^2\le\dfrac{9}{4}\Leftrightarrow NL\le\dfrac{3}{2}\).Dấu "=" khi \(a=b=c\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2021
Đặt \(\left(\sqrt{a};\sqrt{b};\sqrt{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=1\)
BĐT trở thành: \(\dfrac{xy}{\sqrt{x^2+y^2+2z^2}}+\dfrac{yz}{\sqrt{y^2+z^2+2x^2}}+\dfrac{zx}{\sqrt{x^2+z^2+2y^2}}\le\dfrac{1}{2}\)
Ta có:
\(x^2+z^2+y^2+z^2\ge\dfrac{1}{2}\left(x+z\right)^2+\dfrac{1}{2}\left(y+z\right)^2\ge\left(x+z\right)\left(y+z\right)\)
\(\Rightarrow\dfrac{xy}{\sqrt{x^2+y^2+2z^2}}\le\dfrac{xy}{\sqrt{\left(x+z\right)\left(y+z\right)}}\le\dfrac{1}{2}\left(\dfrac{xy}{x+z}+\dfrac{xy}{y+z}\right)\)
Tương tự: \(\dfrac{yz}{\sqrt{y^2+z^2+2x^2}}\le\dfrac{1}{2}\left(\dfrac{yz}{x+y}+\dfrac{yz}{x+z}\right)\)
\(\dfrac{zx}{\sqrt{z^2+x^2+2y^2}}\le\dfrac{1}{2}\left(\dfrac{zx}{x+y}+\dfrac{zx}{y+z}\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(\dfrac{zx+yz}{x+y}+\dfrac{xy+zx}{y+z}+\dfrac{yz+xy}{z+x}\right)=\dfrac{1}{2}\left(x+y+z\right)=\dfrac{1}{2}\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z\) hay \(a=b=c\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 8 2021
\(\dfrac{\sqrt{ab}}{a+c+b+c}\le\dfrac{\sqrt{ab}}{2\sqrt{\left(a+c\right)\left(b+c\right)}}\le\dfrac{1}{4}\left(\dfrac{a}{a+c}+\dfrac{b}{b+c}\right)\)
Tương tự và cộng lại:
\(A\le\dfrac{1}{4}\left(\dfrac{a}{a+c}+\dfrac{b}{b+c}+\dfrac{b}{a+b}+\dfrac{c}{a+c}+\dfrac{a}{a+b}+\dfrac{c}{b+c}\right)=\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(a=b=c\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1
Bunhiacopxki:
\(\left(b+a+a\right)\left(b+c+\dfrac{c^2}{a}\right)\ge\left(b+\sqrt{ca}+c\right)^2\)
\(\Rightarrow\dfrac{2a^2+ab}{\left(b+\sqrt{ca}+c\right)^2}\ge\dfrac{2a^2+ab}{\left(2a+b\right)\left(b+c+\dfrac{c^2}{a}\right)}=\dfrac{a^2}{c^2+ab+bc}\)
Tương tự:
\(\dfrac{2b^2+bc}{\left(c+\sqrt{ca}+a\right)^2}\ge\dfrac{b^2}{a^2+ab+bc}\)
\(\dfrac{2c^2+ca}{\left(a+\sqrt{bc}+b\right)^2}\ge\dfrac{c^2}{b^2+ac+bc}\)
\(\Rightarrow P\ge\dfrac{a^2}{c^2+ab+ac}+\dfrac{b^2}{a^2+ab+bc}+\dfrac{c^2}{b^2+ac+bc}\)
\(\Rightarrow P\ge\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2+2ab+2bc+2ca}=1\)
Dấu "=" xảy ra khi \(a=b=c\)
30 tháng 12 2021
\(\dfrac{ab}{\sqrt{ab+2c}}=\dfrac{ab}{\sqrt{ab+\left(a+b+c\right)c}}=\dfrac{ab}{\sqrt{\left(a+c\right)\left(b+c\right)}}=ab\cdot\sqrt{\dfrac{1}{a+b}\cdot\dfrac{1}{b+c}}\le ab\cdot\dfrac{1}{2}\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)=\dfrac{1}{2}\left(\dfrac{ab}{a+b}+\dfrac{ab}{b+c}\right)\)
CMTT: \(\dfrac{bc}{\sqrt{bc+2a}}\le\dfrac{1}{2}\left(\dfrac{bc}{a+b}+\dfrac{bc}{a+c}\right);\dfrac{ac}{\sqrt{ac+2b}}\le\dfrac{1}{2}\left(\dfrac{ac}{b+c}+\dfrac{ac}{b+a}\right)\)
\(\Leftrightarrow P\le\dfrac{1}{2}\left(\dfrac{ab}{c+a}+\dfrac{ab}{c+b}+\dfrac{bc}{b+a}+\dfrac{bc}{c+a}+\dfrac{ac}{b+c}+\dfrac{ac}{b+c}\right)\\ \Leftrightarrow P\le\dfrac{1}{2}\left[\dfrac{b\left(a+c\right)}{a+c}+\dfrac{a\left(b+c\right)}{b+c}+\dfrac{c\left(a+b\right)}{a+b}\right]=\dfrac{1}{2}\left(a+b+c\right)=1\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{2}{3}\)
30 tháng 8 2021
\(VT=\sqrt{\dfrac{a^2b^2}{c\left(a+b+c\right)+ab}}+\sqrt{\dfrac{b^2c^2}{a\left(a+b+c\right)+bc}}+\sqrt{\dfrac{a^2c^2}{b\left(a+b+c\right)+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{ac+ab+bc+c^2}}+\sqrt{\dfrac{b^2c^2}{a^2+ac+ab+bc}}+\sqrt{\dfrac{a^2c^2}{ab+bc+b^2+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{\left(c+a\right)\left(b+c\right)}}+\sqrt{\dfrac{a^2c^2}{\left(b+c\right)\left(a+b\right)}}+\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\)
Áp dụng BĐT Cauchy-Schwarz:
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\le\dfrac{\dfrac{bc}{a+b}+\dfrac{bc}{a+c}}{2}\\\sqrt{\dfrac{a^2c^2}{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\dfrac{ca}{a+b}+\dfrac{ca}{b+c}}{2}\\\sqrt{\dfrac{a^2b^2}{\left(b+c\right)\left(a+c\right)}}\le\dfrac{\dfrac{ab}{b+c}+\dfrac{ab}{a+c}}{2}\end{matrix}\right.\)
\(\Rightarrow VT\le\dfrac{\left(\dfrac{bc}{a+b}+\dfrac{ca}{a+b}\right)+\left(\dfrac{ca}{b+c}+\dfrac{ab}{b+c}\right)+\left(\dfrac{bc}{a+c}+\dfrac{ab}{a+c}\right)}{2}\\ \Rightarrow VT\le\dfrac{a+b+c}{2}=\dfrac{2}{2}=1\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{2}{3}\)
27 tháng 10 2021
TK: Cho các số thực dương a, b, c thỏa mãn a + b+ c = 3. Chứng minh rằng: \(\sqrt{2a^2+\frac{7}{b^2}}+\sqrt{2b^2+\frac{7}{... - Hoc24
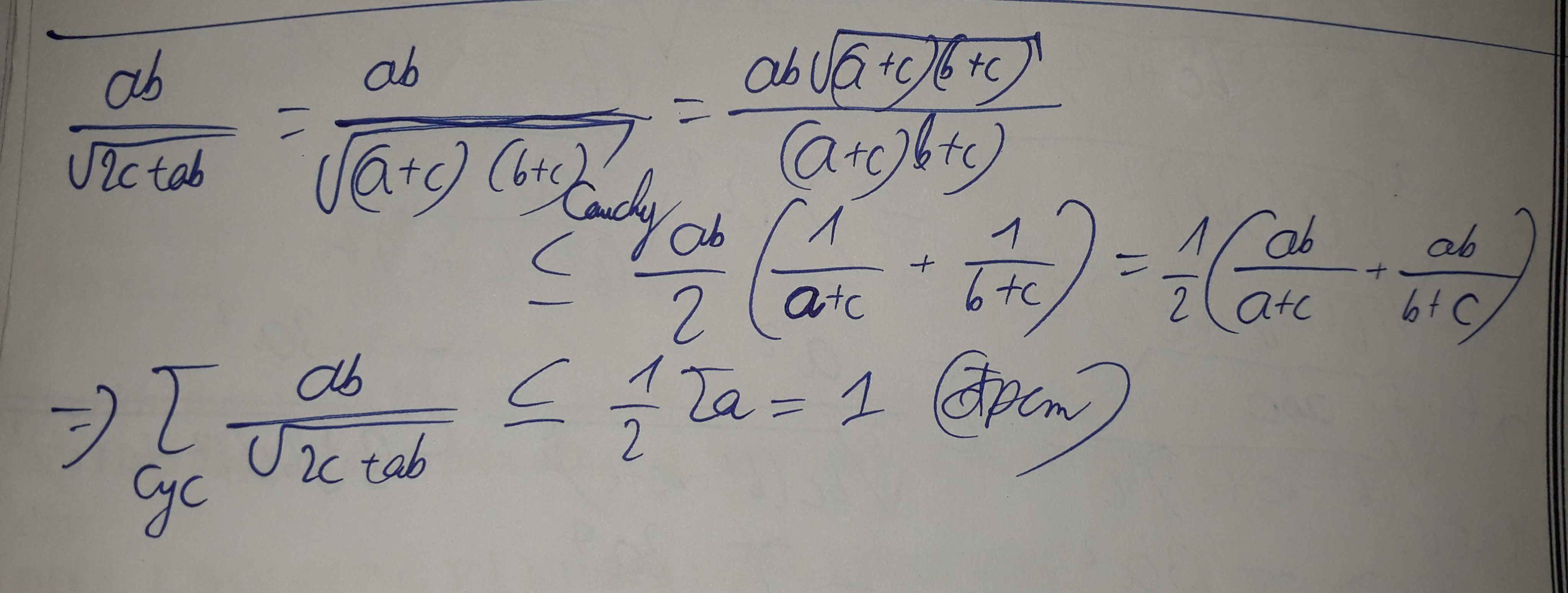
Lời giải:
Đặt biểu thức đã cho là $A$
Ta có:
\(A=\sqrt{\frac{a}{b+c+2a}}+\sqrt{\frac{b}{a+c+2b}}+\sqrt{\frac{c}{a+b+2c}}\)
\(A=\sqrt{\frac{a}{(a+b)+(a+c)}}+\sqrt{\frac{b}{(b+c)+(b+a)}}+\sqrt{\frac{c}{(c+a)+(c+b)}}\)
Áp dụng BĐT AM-GM:
\(A\leq\sqrt{\frac{a}{2\sqrt{(a+b)(a+c)}}}+\sqrt{\frac{b}{2\sqrt{(b+c)(b+a)}}}+\sqrt{\frac{c}{2\sqrt{(c+a)(c+b)}}}\)
\(\Leftrightarrow A\leq \sqrt[4]{\frac{a^2}{4(a+b)(a+c)}}+\sqrt[4]{\frac{b^2}{4(b+c)(b+a)}}+\sqrt[4]{\frac{c^2}{4(c+a)(c+b)}}(*)\)
Tiếp tục áp dụng AM-GM:
\(\sqrt[4]{\frac{a^2}{4(a+b)(a+c)}}\leq \frac{1}{4}\left(\frac{a}{a+b}+\frac{a}{a+c}+\frac{1}{2}+\frac{1}{2}\right)\)
\(\sqrt[4]{\frac{b^2}{4(b+c)(b+a)}}\leq \frac{1}{4}\left(\frac{b}{b+c}+\frac{b}{a+b}+\frac{1}{2}+\frac{1}{2}\right)\)
\(\sqrt[4]{\frac{c^2}{4(c+a)(c+b)}}\leq \frac{1}{4}\left(\frac{c}{c+a}+\frac{c}{c+b}+\frac{1}{2}+\frac{1}{2}\right)\)
Cộng theo vế kết hợp với $(*)$
\(\Rightarrow A\leq \frac{1}{4}\left(\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}+6.\frac{1}{2}\right)\)
\(\Leftrightarrow A\leq \frac{1}{4}.6=\frac{3}{2}\)
Vậy \(A_{\max}=\frac{3}{2}\Leftrightarrow a=b=c\)
\(a=b=c\rightarrow P=\frac{3}{2}\). Ta se c/m do la gtln của P. Thật vậy:
\(\frac{1}{2}P=\sqrt{\frac{1}{4}.\frac{a}{b+c+2a}}+...\)
\(\le\frac{1}{2}\left(\frac{1}{4}+\frac{a}{b+c+2a}+\frac{1}{4}+\frac{b}{c+a+2b}+\frac{1}{4}+\frac{c}{a+b+2c}\right)\)
\(=\frac{1}{2}\left(\frac{3}{4}+\frac{a}{\left(b+a\right)+\left(c+a\right)}+\frac{b}{\left(c+b\right)+\left(b+a\right)}+\frac{c}{\left(c+a\right)+\left(c+b\right)}\right)\)
\(\le\frac{1}{2}\left[\frac{3}{4}+\frac{1}{4}\left(\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}\right)\right]=\frac{3}{4}\)
Do đó \(P\le\frac{3}{2}\)
Đẳng thức xảy ra khi a = b = c