cho ba số a,b,c là các số dương thoả mãn abc=1.chứng minh rằng:\(\dfrac{a}{\left(ab+a+1\right)^2}+\dfrac{b}{\left(bc+c+1\right)^2}+\dfrac{c}{\left(ac +c+1\right)^2}\ge\dfrac{1}{a+b+c}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 3 2022
Bất đẳng thức sai, chẳng hạn với \(a=b=10^{-4};c=0,5-a-b\).
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 8 2021
\(3=ab+bc+ca\ge3\sqrt[3]{\left(abc\right)^2}\Rightarrow abc\le1\)
\(\dfrac{1}{1+a^2\left(b+c\right)}=\dfrac{1}{1+a\left(ab+ac\right)}=\dfrac{1}{1+a\left(3-bc\right)}=\dfrac{1}{1+3a-abc}=\dfrac{1}{3a+\left(1-abc\right)}\le\dfrac{1}{3a}\)
Tương tự và cộng lại:
\(VT\le\dfrac{1}{3a}+\dfrac{1}{3b}+\dfrac{1}{3c}=\dfrac{ab+bc+ca}{3abc}=\dfrac{3}{3abc}=\dfrac{1}{abc}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 8 2021
\(a+\dfrac{1}{a+1}=\dfrac{a^2+a+1}{a+1}=\dfrac{4a^2+4a+4}{4\left(a+1\right)}=\dfrac{3\left(a+1\right)^2+\left(a-1\right)^2}{4\left(a+1\right)}\ge\dfrac{3\left(a+1\right)^2}{4\left(a+1\right)}=\dfrac{3}{4}\left(a+1\right)\ge\dfrac{3}{2}\sqrt{a}\)
Tương tự: \(b+\dfrac{1}{b+1}\ge\dfrac{3}{2}\sqrt{b}\) ; \(c+\dfrac{1}{c+1}\ge\dfrac{3}{2}\sqrt{c}\)
Nhân vế:
\(VT\ge\dfrac{27}{8}\sqrt{abc}\ge\dfrac{27}{8}\) (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 2 2022
Đặt \(a\left(1-b\right)=x;b\left(1-c\right)=y;c\left(1-a\right)=x\)
\(\Rightarrow1-\left(a+b+c\right)+ab+bc+ca=1-a\left(1-b\right)-b\left(1-c\right)-c\left(1-a\right)=1-x-y-z\)
BĐT cần c/m trở thành:
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{3}{1-x-y-z}\)
\(\Leftrightarrow\left(1-x-y-z\right)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)-3\ge0\)
\(\Leftrightarrow\dfrac{1-x-y-z}{x}+\dfrac{1-x-y-z}{y}+\dfrac{1-x-y-z}{z}-3\ge0\)
\(\Leftrightarrow\dfrac{1-y-z}{x}+\dfrac{1-z-x}{y}+\dfrac{1-x-y}{z}-6\ge0\) (1)
Lại có: \(1-y-z=1-b\left(1-c\right)-c\left(1-a\right)=1-b-c+bc+ca=\left(1-b\right)\left(1-c\right)+ca\)
Nên (1) tương đương:
\(\dfrac{\left(1-b\right)\left(1-c\right)+ca}{a\left(1-b\right)}+\dfrac{\left(1-a\right)\left(1-c\right)+ab}{b\left(1-c\right)}+\dfrac{\left(1-a\right)\left(1-b\right)+bc}{c\left(1-a\right)}-6\ge0\)
\(\Leftrightarrow\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\)
BĐT trên hiển nhiên đúng theo AM-GM do:
\(\dfrac{1-c}{a}+\dfrac{c}{1-b}+\dfrac{1-a}{b}+\dfrac{a}{1-c}+\dfrac{1-b}{c}+\dfrac{b}{1-a}\ge6\sqrt[6]{\dfrac{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}{abc\left(1-a\right)\left(1-b\right)\left(1-c\right)}}=6\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{2}\)
19 tháng 2 2022
Cám ơn bài giải của thầy Lâm ạ!
Và từ bài bất đăng thức này, đã được chế thành bài toán hình học trong 1 kì thi học sinh giỏi toán cấp tỉnh thầy ạ!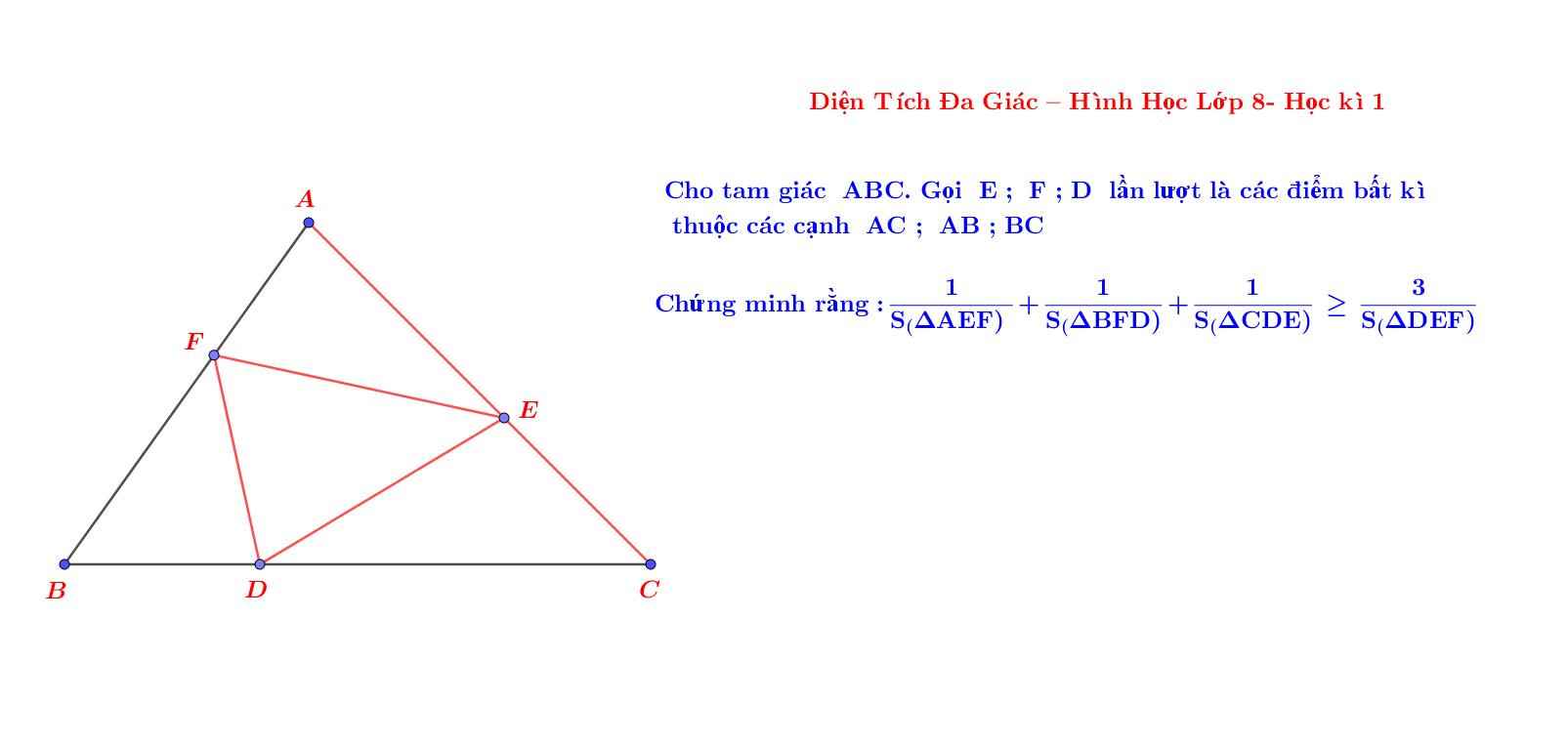
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2023
Tách biểu thức như sau:
\(\left(\dfrac{a}{9}+\dfrac{b}{12}+\dfrac{c}{6}+\dfrac{8}{abc}\right)+\left(\dfrac{a}{18}+\dfrac{b}{24}+\dfrac{2}{ab}\right)+\left(\dfrac{b}{16}+\dfrac{c}{8}+\dfrac{2}{bc}\right)+\left(\dfrac{a}{9}+\dfrac{c}{6}+\dfrac{2}{ca}\right)+\left(\dfrac{13a}{18}+\dfrac{13b}{24}\right)+\left(\dfrac{13b}{48}+\dfrac{13c}{24}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2023
Đầu tiên em phải dự đoán được điểm rơi (các cặp a;b;c đẹp sao cho \(ab=12\) và \(bc=8\), có các bộ là \(\left(6;2;4\right);\left(3;4;2\right)\)
Sau đó thay 2 bộ kia vào P xem cái nào bằng \(\dfrac{121}{12}\) thì nó đúng (ở đây là 3;4;2)
Khi có điểm rơi, bây giờ chỉ cần tính toán và ghép theo AM-GM để khử tử- mẫu
Cần ghép \(\dfrac{8}{abc}+\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}\) (AM-GM 4 số sẽ khử hết biến)
\(\dfrac{8}{abc}=\dfrac{8}{3.4.2}=\dfrac{1}{3}\)
Do đó \(\dfrac{3}{x}=\dfrac{4}{y}=\dfrac{2}{z}=\dfrac{1}{3}\Rightarrow x=9;y=12;z=6\)
Hay ta có bộ đầu tiên: \(\dfrac{a}{9}+\dfrac{b}{12}+\dfrac{c}{6}+\dfrac{8}{abc}\)
Tương tự cho các biến dưới mẫu còn lại, phần dư cuối cùng sẽ ghép cặp a với b (tận dụng \(ab\ge12\)) và b với c, nó sẽ tự đủ
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
\(\dfrac{a^3}{\left(b+1\right)\left(c+2\right)}+\dfrac{b+1}{12}+\dfrac{c+2}{18}\ge3\sqrt[3]{\dfrac{a^3\left(b+1\right)\left(c+2\right)}{216\left(b+1\right)\left(c+2\right)}}=\dfrac{a}{2}\)
Tương tự: \(\dfrac{b^3}{\left(c+1\right)\left(a+2\right)}+\dfrac{c+1}{12}+\dfrac{a+2}{18}\ge\dfrac{b}{2}\)
\(\dfrac{c^3}{\left(a+1\right)\left(b+2\right)}+\dfrac{a+1}{12}+\dfrac{b+2}{18}\ge\dfrac{c}{2}\)
Cộng vế:
\(VT+\dfrac{5}{36}\left(a+b+c\right)+\dfrac{7}{12}\ge\dfrac{1}{2}\left(a+b+c\right)\)
\(\Rightarrow VT\ge\dfrac{13}{36}\left(a+b+c\right)-\dfrac{7}{12}\ge\dfrac{13}{36}.3\sqrt[3]{abc}-\dfrac{7}{12}=\dfrac{1}{2}\) (đpcm)
MS
13 tháng 1 2018
Ta có:
\(\dfrac{1}{a^3\left(b+c\right)}+\dfrac{1}{b^3\left(c+a\right)}+\dfrac{1}{c^3\left(a+b\right)}\ge\dfrac{3}{2}\)
\(\dfrac{1^2}{a^3\left(b+c\right)}+\dfrac{1^2}{b^3\left(c+a\right)}+\dfrac{1^2}{c^3\left(a+b\right)}\ge\dfrac{3}{2}\)
\(\dfrac{a^2b^2c^2}{a^3\left(b+c\right)}+\dfrac{a^2b^2c^2}{b^3\left(c+a\right)}+\dfrac{a^2b^2c^2}{c^3\left(a+b\right)}\ge\dfrac{3}{2}\)
\(\dfrac{b^2c^2}{a\left(c+b\right)}+\dfrac{a^2c^2}{b\left(c+a\right)}+\dfrac{a^2b^2}{c\left(a+b\right)}\ge\dfrac{3}{2}\)
Áp dụng BĐT Svacxo ta có:
\(\dfrac{b^2c^2}{a\left(b+c\right)}+\dfrac{a^2c^2}{b\left(c+a\right)}+\dfrac{a^2b^2}{c\left(a+b\right)}\ge\dfrac{\left(ab+bc+ca\right)^2}{a\left(b+c\right)+b\left(a+c\right)+c\left(a+b\right)}\) \(\dfrac{b^2c^2}{a\left(b+c\right)}+\dfrac{a^2c^2}{b\left(c+a\right)}+\dfrac{a^2b^2}{c\left(a+b\right)}\ge\dfrac{\left(ab+bc+ca\right)}{2}\) (1)
Chứng minh: \(\dfrac{ab+bc+ca}{2}\ge\dfrac{3}{2}\Leftrightarrow ab+bc+ca\ge3\)
Áp dụng BĐT Cosi ta có:
\(ab+bc+ca\ge3\sqrt[3]{ab.bc.ca}\)
\(ab+bc+ca\ge3\) (2)
Từ (1) và (2)
=> ĐPCM
HQ
20 tháng 2 2021
Đặt\(P=\dfrac{a}{1+b^2}+\dfrac{b}{1+c^2}+\dfrac{c}{1+a^2+}+\dfrac{1}{2}\left(ab+bc+ca\right)\)
Bổ đề: \(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge9\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{9}{a+b+c}\) (1)
Chứng minh bổ đề: \(\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge9\sqrt[3]{abc.\dfrac{1}{abc}}=9\left(\forall a,b,c\ge0\right)\)
Kết hợp điều kiện đề bài ta được: \(a+b+c\ge3\)
Ta có: \(\dfrac{ab^2}{1+b^2}\le\dfrac{ab^2}{2\sqrt{b^2}}=\dfrac{ab}{2}\) ( AM-GM cho 2 số không âm 1 và b^2 )
\(\Rightarrow\dfrac{a}{1+b^2}=a-\dfrac{ab^2}{1+b^2}\ge a-\dfrac{ab}{2}\left(1\right)\)
Chứng minh hoàn toàn tương tự: \(\dfrac{b}{1+c^2}\ge b-\dfrac{bc}{2}\left(2\right)\)
\(\dfrac{c}{1+a^2}\ge c-\dfrac{ca}{2}\left(3\right)\)
Cộng (1),(2),(3) vế theo vế thu được: \(P\ge a+b+c=3\)
Dấu "=" xảy ra tại a=b=c=1
iải của
Áp dụng BĐT Cauchy-Schwarz ta có:
\((ab+a+1)^2 \le (a+b+c) \left( a+ a^2b+ \frac 1c \right) = (a+b+c)(a+a^2b+ab)\)
\(\Rightarrow \dfrac{a}{(ab+a+1)^2} \ge \dfrac{a}{(a+b+c)(a+a^2b+ab)}= \dfrac{1}{(a+b+c)(1+ab+b)}\)
Thiết lập các BĐT tương tự rồi cộng theo vế ta có:
\(\sum \dfrac{a}{(ab+a+1)^2} \ge \dfrac{1}{a+b+c} \sum \dfrac{1}{ab+b+1}= \dfrac{1}{a+b+c}\)
c2: Áp dụng BĐT bunyakovsky:
\(\left(a+b+c\right)\left[\dfrac{a}{\left(ab+a+1\right)^2}+\dfrac{b}{\left(bc+b+1\right)^2}+\dfrac{c}{\left(ac+c+1\right)^2}\right]\ge\left(\dfrac{a}{ab+a+1}+\dfrac{b}{bc+b+1}+\dfrac{c}{ca+c+1}\right)^2\)
Xét \(\dfrac{a}{ab+a+1}+\dfrac{b}{bc+b+1}+\dfrac{c}{ac+c+1}=\dfrac{a}{ab+a+1}+\dfrac{ab}{1+ab+a}+\dfrac{c}{c\left(a+1+ab\right)}\)
\(=\dfrac{ab+a+1}{ab+a+1}=1\)
do đó \(\left(a+b+c\right).VT\ge1\Leftrightarrow VT\ge\dfrac{1}{a+b+c}\)
dấu = xảy ra khi a=b=c=1