K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dưới đây là một vài câu hỏi có thể liên quan tới câu hỏi mà bạn gửi lên. Có thể trong đó có câu trả lời mà bạn cần!

CM
25 tháng 5 2017
a, HS tự làm
b, Chú ý hai đường phân giác trong và ngoài tại một đỉnh vuông góc nhau
c, Chú ý BM là phân giác góc ABC. Từ đó tính được số đo các góc của tam giác MAB và suy ra ĐPCM
Chú ý Hai tam giác MAB và ABC đều là các tam giác nửa đều
Từ đó tính được tỉ số đồng dạng là 1/2

CM
27 tháng 3 2019
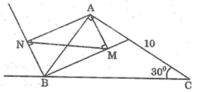

Suy ra: MN // BC (có cặp góc so le trong bằng nhau)
Vì AMBN là hình chữ nhật nên AB = MN

11 tháng 8 2021
a) Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A

a. Trong tam giác vuông ABC, ta có :
\(AB=BC.\sin\widehat{C}=10.\sin30^o=10.\frac{1}{2}=5\left(cm\right)\)
\(AC=BC.\cos\widehat{C}=10.\cos30^o=10.\frac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
b)
Ta có : \(BM\perp BN\)( tính chất 2 góc kề bù ) \(\Rightarrow\widehat{MBN}=90^o\left(1\right)\)
\(AM\perp BM\left(gt\right)\Rightarrow\widehat{AMB}=90^o\left(2\right)\)
\(AN\perp BN\left(gt\right)\Rightarrow\widehat{ANB}=90^o\left(3\right)\)
Từ (1) (2) và (3) , suy ra : tứ giác AMBN là hình chữ nhật
\(\Rightarrow\Delta AMB=\Delta NBM\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{NMB}\)
Mà \(\widehat{ABM}=\widehat{MBC}\left(gt\right)\)
\(\Rightarrow\widehat{NMB}=\widehat{NBC}\)
Suy ra: MN // BC (có cặp góc so le trong bằng nhau)
Vì AMBN là hình chữ nhật nên AB = MN
)): gửi cả câu c) rồi mà cuối cùng lại 0 có , làm lại câu c) sang bên này :>
c)
Tam giác ABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
\(\Rightarrow\widehat{B}=90^o-\widehat{C}=90^o-30^o=60^o\)
\(\Rightarrow\widehat{ABM}=\frac{1}{2}\widehat{B}=\frac{1}{2}.60^o=30^o\)
Xét 2 tam giác ABC và MAB ,, ta có :
\(\widehat{BAC}=\widehat{AMB}=90^o\)
\(\widehat{ACB}=\widehat{ABM}=90^o\)
\(\Rightarrow\Delta ABC~\Delta MAB\left(g.g\right)\)
=> Tỉ số đồng dạnh \(k=\frac{AB}{BC}=\frac{5}{10}=\frac{1}{2}\)