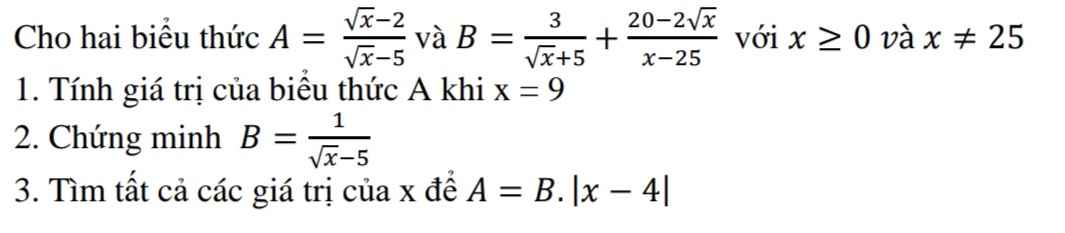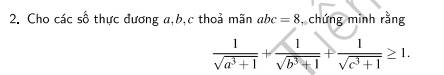K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dưới đây là một vài câu hỏi có thể liên quan tới câu hỏi mà bạn gửi lên. Có thể trong đó có câu trả lời mà bạn cần!
5B
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
6
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 10 2021
Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)
7 tháng 9 2021
3: Ta có: A=B|x-4|
\(\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}-5}:\dfrac{1}{\sqrt{x}-5}=\left|x-4\right|\)
\(\Leftrightarrow\left|x-4\right|=\sqrt{x}-2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=\sqrt{x}-2\left(x\ge4;x\ne25\right)\\x-4=2-\sqrt{x}\left(0< x< 4\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-\sqrt{x}-2=0\\x+\sqrt{x}-6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=4\left(loại\right)\end{matrix}\right.\)
7 tháng 9 2021
1: Thay x=9 vào A, ta được:
\(A=\dfrac{3-2}{3-5}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
2: Ta có: \(B=\dfrac{3}{\sqrt{x}+5}+\dfrac{20-2\sqrt{x}}{x-25}\)
\(=\dfrac{3\sqrt{x}-15+20-2\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(=\dfrac{1}{\sqrt{x}-5}\)
18 tháng 11 2023
Đặt \(a=\dfrac{x}{2};b=\dfrac{y}{2};c=\dfrac{z}{2}\). Khi đó \(xyz=1\).
Bất đẳng thức cần chứng minh trở thành:
\(\sum\dfrac{1}{\sqrt{8x^3+1}}\ge1\)
Ta có: \(\sum\dfrac{1}{\sqrt{8x^3+1}}=\sum\sqrt{\dfrac{b^3c^3}{8+b^3c^3}}=\sum\dfrac{b^2c^2}{\sqrt{8bc+b^4c^4}}\ge\dfrac{\left(ab+bc+ca\right)^2}{\sum\sqrt{8bc+b^4c^4}}=\dfrac{\sum b^2c^2+2\sum a}{\sum\sqrt{8bc+b^4c^4}}\ge\dfrac{\sum b^2c^2+6}{\sum\sqrt{8bc+b^4c^4}}\)
Phép chứng minh sẽ hoàn tất nếu ta chứng minh được:
\(\sum b^2c^2+6\ge\sum\sqrt{8bc+b^4c^4}\left(\cdot\right)\)
Để ý rằng, nếu ta chứng minh được \(b^2c^2+2\ge\sqrt{8bc+b^4c^4}\left(1\right)\) thì ta sẽ chứng minh được (*).
Thật vậy, bằng phép biến đổi tương đương, ta có:
\(b^2c^2+2\ge\sqrt{8bc+b^4c^4}\)
\(\Leftrightarrow b^4c^4+4b^2c^2+4\ge8bc+b^4c^4\)
\(\Leftrightarrow4\left(bc-1\right)^2\ge0\) (luôn đúng).
Vậy nhận xét (1) là đúng. Từ đây ta có điều phải chứng minh.
Dấu "=" xảy ra khi \(a=b=c=2\)
18 tháng 11 2023
Đặt \(A=\dfrac{1}{\sqrt{a^3+1}}+\dfrac{1}{\sqrt{b^3+1}}+\dfrac{1}{\sqrt{c^3+1}}\)
\(\sqrt{a^3+1}=\sqrt{\left(a+1\right)\left(a^2-a+1\right)}\)
=>\(\sqrt{a^3+1}< =\dfrac{a+1+a^2-a+1}{2}=\dfrac{a^2+2}{2}\)
=>\(\dfrac{1}{\sqrt{a^3+1}}>=\dfrac{2}{a^2+2}\)
Chứng minh tương tự, ta được:
\(\sqrt{b^3+1}< =\dfrac{b^2+2}{2}\) và \(\sqrt{c^3+1}< =\dfrac{c^2+2}{2}\)
=>\(\dfrac{1}{\sqrt{b^3+1}}>=\dfrac{2}{b^2+2};\dfrac{1}{\sqrt{c^3+1}}>=\dfrac{2}{c^2+2}\)
=>\(\dfrac{1}{\sqrt{a^3+1}}+\dfrac{1}{\sqrt{b^3+1}}+\dfrac{1}{\sqrt{c^3+1}}>=\dfrac{2}{a^2+2}+\dfrac{2}{b^2+2}+\dfrac{2}{c^2+2}\)
=>\(A>=\dfrac{2}{a^2+2}+\dfrac{2}{b^2+2}+\dfrac{2}{c^2+2}\)
=>\(A>=\dfrac{2\left(b^2+2\right)\left(c^2+2\right)+2\left(a^2+2\right)\left(c^2+2\right)+2\left(b^2+2\right)\left(a^2+2\right)}{\left(a^2+2\right)\left(c^2+2\right)\left(b^2+2\right)}\)
=>\(A>=\dfrac{2\left(b^2c^2+2c^2+2b^2+4+a^2c^2+2a^2+2c^2+4+a^2b^2+2b^2+2a^2+4\right)}{\left(a^2+2\right)\left(b^2+2\right)\left(c^2+2\right)}\)
=>\(A>=\dfrac{2\left(a^2b^2+b^2c^2+c^2a^2\right)+8\left(a^2+b^2+c^2\right)+24}{\left(a^2+2\right)\left(b^2+2\right)\left(c^2+2\right)}\)
=>\(A>=\dfrac{2\left(a^2b^2+b^2c^2+a^2c^2\right)+4\left(a^2+b^2+c^2\right)+24+4\left(a^2+b^2+c^2\right)}{2\left(a^2b^2+b^2c^2+a^2c^2\right)+4\left(a^2+b^2+c^2\right)+8+8^2}\)(Vì abc=8)
Ta lại có: \(a^2+b^2+c^2>=3\sqrt[3]{a^2b^2c^2}=3\cdot\sqrt[3]{8^2}=12\)
=>\(4\left(a^2+b^2+c^2\right)>=48\)
=>\(A>=\dfrac{2\left(a^2b^2+b^2c^2+a^2c^2\right)+4\left(a^2+b^2+c^2\right)+24+48}{2\left(a^2b^2+b^2c^2+a^2c^2\right)+4\left(a^2+b^2+c^2\right)+8+64}\)
=>A>=1(ĐPCM)