Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bình phương 2 vế ta được
3a2 + 18 - 2a2 - 4ab - 2b2 \(\ge\)0
<=> a2 - 2b2 - 4ab + 3( a2 + b2) \(\ge0\)
<=> 4a2 - 4ab + b2 \(\ge0\)
<=> (2a - b)2 \(\ge0\)(đúng)
ta có: \(\sqrt{3\left(a^2+b^2\right)}\ge\left(a+b\right)^2\sqrt{2}\)
\(\Leftrightarrow3\left(2a^2+b^2\right)\ge2\left(a+b\right)^2\)(vì a2+b2=6)
\(\Leftrightarrow6a^2+3b^2\ge2a^2+4ab+2b^2\)
\(\Leftrightarrow4a^2-4ab+b^2\ge0\\ \Leftrightarrow\left(2a-b\right)^2\ge0\)
(luôn đúng với mọi a;bdương)
=> đpcm
\(\left(a+3b\right)\left(b+3a\right)\le\left(\frac{4a+4b}{2}\right)^2=\left(2a+2b\right)^2\)
=>\(\frac{1}{2}\sqrt{\left(a+3b\right)\left(b+3a\right)}\le\frac{1}{2}\left(2a+2b\right)=a+b\)
Mình làm phần dễ nhất rồi, còn lại của bạn đó ^^
\(=\)\(18\left(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}\right)\)\(=\)\(18\frac{3}{1}\)\(>\)\(\left(9+5\sqrt{3}\right)\left(a^2+b^2+c^2\right)\)\(=\)\(0\)
Vậy\(18\frac{3}{1}\)\(>\)\(0\)
Chứng minh là \(18\frac{3}{1}\)\(>\)\(0\)là đúng
chúc bạn học tốt
Bất đẳng thức trên
<=> 
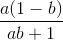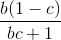+ 1 + 
+ 1 +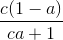 
+ 1 ≥ 3
<=> 
+ 
+ 
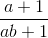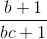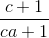≥ 3 (*)
Ta có: VT(*) ≥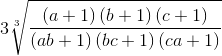 
Ta sẽ chứng minh: (a + 1)(b + 1)(c + 1) ≥ (ab + 1)(bc + 1)(ca + 1)
<=> abc + ab + bc + ca + a + b + c + 1
≥ a2b2c2 + abc(a + b + c) + ab + bc + ca + 1
<=> 3 ≥ a2b2c2 + 2abc (**)
Theo Cosi: 3 = a + b + c ≥ 3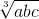
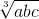=> ≤ 1 => abc ≤ 1
Vậy (**) đúng => (*) đúng.
\(\sqrt{3\left(a^2+6\right)}\ge\sqrt{2}\left(a+b\right)\)
\(\Leftrightarrow\sqrt{3\left(2a^2+b^2\right)}\ge\sqrt{2}\left(a+b\right)\)
\(\Leftrightarrow6a^2+3b^2\ge2a^2+4ab+2b^2\)
\(\Leftrightarrow4a^2-4ab+b^2\ge0\)
\(\Leftrightarrow\left(2a-b\right)^2\ge0\)(đúng)
=> ĐPCM
cho a,b là 2 số dương thỏa mãn a2+b2=6
cmr \(\sqrt{3\left(a^2+6\right)}\ge\left(a+b\right)\sqrt{2}\)
Ta có:
\(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}=\frac{\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2-\left(a+b+c\right)}{2}=\frac{9-5}{2}=2\)
Suy ra \(a+2=a+\sqrt{ab}+\sqrt{bc}+\sqrt{ca}=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{c}+\sqrt{a}\right)\)
Tương tự, ta áp dụng với hai biến thực dương còn lại, thu được:
\(\hept{\begin{cases}b+2=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\\c+2=\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{c}+\sqrt{a}\right)\end{cases}}\)
Khi đó, ta nhân vế theo vế đối với ba đẳng thức trên, nhận thấy: \(\left(a+2\right)\left(b+2\right)\left(c+2\right)=\left[\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{c}+\sqrt{a}\right)\right]^2\)
\(\Rightarrow\) \(\sqrt{\left(a+2\right)\left(b+2\right)\left(c+2\right)}=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{c}+\sqrt{a}\right)\) (do \(a,b,c>0\) )
nên \(\frac{\sqrt{a}}{a+2}+\frac{\sqrt{b}}{b+2}+\frac{\sqrt{c}}{c+2}=\frac{\sqrt{a}\left(\sqrt{b}+\sqrt{c}\right)+\sqrt{b}\left(\sqrt{c}+\sqrt{a}\right)+\sqrt{c}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{c}+\sqrt{a}\right)}\)
\(=\frac{2\left(\sqrt{ab}+\sqrt{ca}+\sqrt{ca}\right)}{\sqrt{\left(a+2\right)\left(b+2\right)\left(c+2\right)}}=\frac{4}{\sqrt{\left(a+2\right)\left(b+2\right)\left(c+2\right)}}\)
\(\Rightarrow\) \(đpcm\)
Lời giải:
Từ ĐKĐB kết hợp BĐT Bunhiacopxky:
\(3(a^2+6)=3(a^2+a^2+b^2)=(1+2)(2a^2+b^2)\geq (\sqrt{2}a+\sqrt{2}b)^2\)
\(\Rightarrow \sqrt{3(a^2+6)}\geq \sqrt{2}(a+b)\) (đpcm)
Dấu "=" xảy ra khi \(\left\{\begin{matrix} a,b>0\\ a^2+b^2=6\\ \frac{1}{\sqrt{2}a}=\frac{\sqrt{2}}{b}\end{matrix}\right.\) hay $a=\sqrt{\frac{6}{5}}; b=2\sqrt{\frac{6}{5}}$