Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C ngồi vào hàng ghế đó sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp C không ngồi cạnh học sinh lớp B bằng?
A. 1/5
B. 4/5
C. 2/15
D. 2/5






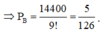
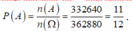
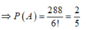

`n(\Omega)=6! =720`
`@TH1:` H/s lớp `C` ngồi đầu tiên hoặc cuối cùng.
`=>` Có `2.1.A_3 ^1 .4! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.
`@TH2:` H/s lớp `C` không ngồi đầu cũng không ngồi cuối.
`=>` Có `4.A_3 ^2 .3! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.
Gọi `A:`" H/s lớp `C` không ngồi cạnh h/s lớp `B`"
`=>n(A)=144.2=288`
`=>P(A)=288/720=2/5`
`->bb D`