Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Ta có 
Giải bất phương trình trên với ẩn |z| ta được:
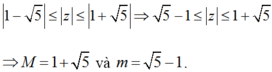
Vậy 
Đáp án C
Giả thiết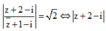 
Đặt 
khi đó
=> Do đó tập hợp điểm biễu diễn z là đường tròn tâm I(0;-3), bán kính R =
10
đặc \(z=a+bi\) (\(a;b\in R\) và \(i^2=-1\))
ta có : \(Y=3\left|z\right|+4\left|z-4i\right|+5\left|z-3\right|\)
\(\Leftrightarrow Y=3\left|a+bi\right|+4\left|a+\left(b-4\right)i\right|+5\left|\left(a-3\right)+bi\right|\)
\(\Leftrightarrow Y=3\sqrt{a^2+b^2}+4\sqrt{a^2+\left(b-4\right)^2}+5\sqrt{\left(a-3\right)^2+b^2}\)
áp dụng bất đẳng thức Bunhiacopxki ta có :
\(Y\ge-\sqrt{\left(3^2+4^2+5^2\right)\left(a^2+b^2+a^2+\left(b-4\right)^2+\left(a-3\right)^2+b^2\right)}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3a^2+3b^2-8b-6a+25}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3\left(a-1\right)^2+\left(\sqrt{3}b-\dfrac{8}{2\sqrt{3}}\right)^2+\dfrac{50}{3}}\)
dấu "=" xảy ra khi \(\dfrac{3}{\sqrt{a^2+b^2}}=\dfrac{4}{\sqrt{a^2+\left(b-4\right)^2}}=\dfrac{4}{\sqrt{\left(a-3\right)^2}+b^2}\)
giải ra tìm được \(a;b\) rồi thay ngược trở lại nha
2. Xem tại đây
1. \(P=\frac{1}{\sqrt{x.1}}+\frac{1}{\sqrt{y.1}}+\frac{1}{\sqrt{z.1}}\)
\(\ge\frac{1}{\frac{x+1}{2}}+\frac{1}{\frac{y+1}{2}}+\frac{1}{\frac{z+1}{2}}\)
\(=\frac{2}{x+1}+\frac{2}{y+1}+\frac{2}{z+1}\ge\frac{2.\left(1+1+1\right)^2}{x+y+z+3}=\frac{18}{3+3}=3\)
Đẳng thức xảy ra \(\Leftrightarrow x=y=z=1\)
1 ) có cách theo cosi đó
áp dụng cosi cho 3 số dương ta có \(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{x}}+x\ge3\sqrt[3]{\frac{1}{\sqrt{x}}\times\frac{1}{\sqrt{x}}\times x}=3\sqrt[3]{1}=3\)(1)
\(\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{y}}+y\ge3\)(2)
\(\frac{1}{\sqrt{z}}+\frac{1}{\sqrt{z}}+z\ge3\)(3)
cộng các vế của (1),(2),(3), đc \(2\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}}\right)+\left(x+y+z\right)\ge9\Rightarrow2P+3\ge9\Rightarrow P\ge3\)
minP=3 khi x=y=z=1
Đặt A=x^4+y^4+z^4 ,P=x^2+y^2+z^2
Ta có A=(x^2)^2+(y^2)^2+(z^2)^2
Áp dụng bđt Cauchy-Schwarz ta có
3A=[(x^2)^2+(y^2)^2+(z^2)^2](1^2+1^2+1^2) >/ (x^2+y^2+z^2)^2=> A >/ (x^2+y^2+z^2)^2/3
Áp dụng bđt Cauchy-Schwarz lần 2
3P=(x^2+y^2+z^2)(1^2+1^2+1^2) >/ (x+y+z)^2=> P >/ (x+y+z)^2/3 >/ 2^2/3 >/ 4/3
=> A >/ (4/3)^2/3=16/27
Đẳng thức xảy ra <=> x=y=z=2/3
Đáp án B