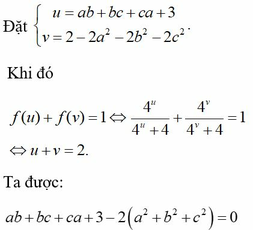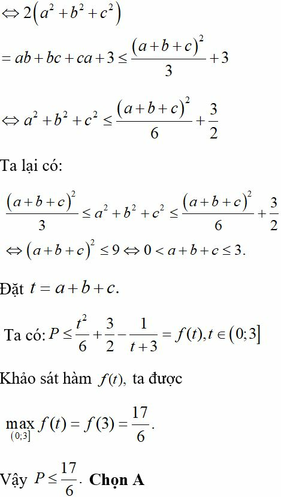Cho a+b+c=0.Chứng minh rằng N=1-(ab+2c2)(bc+2a2)(ca+2b2) là số dương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
I
0
FF
28 tháng 8 2016
3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương.
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết
Vậy nên phải có ít nhất 1 số dương
Không mất tính tổng quát, giả sử a > 0
mà abc > 0 => bc > 0
Nếu b < 0, c < 0:
=> b + c < 0
Từ gt: a + b + c < 0
=> b + c > - a
=> (b + c)^2 < -a(b + c) (vì b + c < 0)
<=> b^2 + 2bc + c^2 < -ab - ac
<=> ab + bc + ca < -b^2 - bc - c^2
<=> ab + bc + ca < - (b^2 + bc + c^2)
ta có:
b^2 + c^2 >= 0
mà bc > 0 => b^2 + bc + c^2 > 0
=> - (b^2 + bc + c^2) < 0
=> ab + bc + ca < 0 (vô lý)
trái gt: ab + bc + ca > 0
Vậy b > 0 và c >0
=> cả 3 số a, b, c > 0
3 tháng 5 2019
1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)
\(\left(b+c\right)^2\ge4b>0\)
\(\left(a+c\right)^2\ge4c>0\)
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)
Mà abc=1
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)
N
17 tháng 9 2017
Biến đổi like that:
\(VT=\sum\dfrac{1}{ab}=\sum\dfrac{ab+bc+ca}{ab}=\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)+3\)
nên chỉ cần :\(\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)\ge\sum\sqrt{\dfrac{1}{a^2}+1}=\sum\dfrac{\sqrt{a^2+1}}{a}\)
Áp dụng AM-GM:
\(\dfrac{\sqrt{a^2+1}}{a}=\dfrac{\sqrt{a^2+ab+bc+ca}}{a}=\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{a}\le\dfrac{2a+b+c}{2a}\)
Áp dụng tương tự:
\(VP=\sum\dfrac{\sqrt{a^2+1}}{a}\le\sum\dfrac{2a+b+c}{2a}=3+\dfrac{1}{2}\sum\left(\dfrac{b}{a}+\dfrac{c}{a}\right)\)
BĐT đúng khi ta chứng minh được
\(VT=\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)\ge3+\dfrac{1}{2}\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)\)
Điều này hiển nhiên đúng theo AM-GM:
\(\dfrac{1}{2}\sum\left(\dfrac{c}{a}+\dfrac{c}{b}\right)=\dfrac{1}{2}\left(\dfrac{c}{a}+\dfrac{c}{b}+\dfrac{a}{b}+\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{b}{c}\right)\ge\dfrac{1}{2}.6\sqrt[6]{\dfrac{a^2b^2c^2}{a^2b^2c^2}}=3\)
\(\Rightarrow\)đpcm
Dấu = xảy ra khi a=b=c
G
22 tháng 7 2019
\(\frac{a+bc}{b+c}+\frac{b+ac}{c+a}+\frac{c+ab}{a+b}\)
\(=\frac{a\left(a+b+c\right)+bc}{b+c}+\frac{b\left(a+b+c\right)+ac}{a+c}+\frac{c\left(a+b+c\right)+ab}{a+b}\)
\(=\frac{\left(a+b\right)\left(a+c\right)}{b+c}+\frac{\left(a+b\right)\left(b+c\right)}{a+c}+\frac{\left(c+a\right)\left(c+b\right)}{a+b}\)
Áp dụng bđt Cô Si: \(\frac{\left(a+b\right)\left(a+c\right)}{b+c}+\frac{\left(a+b\right)\left(b+c\right)}{a+c}\ge2\left(a+b\right)\)
Tương tự,cộng theo vế và rút gọn =>đpcm
2 tháng 4 2020
\(\frac{a+bc}{b+c}+\frac{b+ac}{c+a}+\frac{c+ab}{a+b}\)
\(=\frac{a\left(a+b+c\right)+bc}{b+c}+\frac{b\left(a+b+c\right)+ac}{a+c}+\frac{c\left(a+b+c\right)+ab}{a+b}\)
\(=\frac{\left(a+b\right)\left(a+c\right)}{b+c}+\frac{\left(a+b\right)\left(b+c\right)}{a+c}+\frac{\left(c+a\right)\left(c+b\right)}{a+b}\)
Áp dụng bđt CÔ si
\(\frac{\left(a+b\right)\left(a+c\right)}{b+c}+\frac{\left(a+b\right)\left(b+c\right)}{a+c}\ge2\left(a+b\right)\)
.............
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2020
1. Đề thiếu
2. BĐT cần chứng minh tương đương:
\(a^4+b^4+c^4\ge abc\left(a+b+c\right)\)
Ta có:
\(a^4+b^4+c^4\ge\dfrac{1}{3}\left(a^2+b^2+c^2\right)^2\ge\dfrac{1}{3}\left(ab+bc+ca\right)^2\ge\dfrac{1}{3}.3abc\left(a+b+c\right)\) (đpcm)
3.
Ta có:
\(\left(a^6+b^6+1\right)\left(1+1+1\right)\ge\left(a^3+b^3+1\right)^2\)
\(\Rightarrow VT\ge\dfrac{1}{\sqrt{3}}\left(a^3+b^3+1+b^3+c^3+1+c^3+a^3+1\right)\)
\(VT\ge\sqrt{3}+\dfrac{2}{\sqrt{3}}\left(a^3+b^3+c^3\right)\)
Lại có:
\(a^3+b^3+1\ge3ab\) ; \(b^3+c^3+1\ge3bc\) ; \(c^3+a^3+1\ge3ca\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge3\left(ab+bc+ca\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
\(\Rightarrow VT\ge\sqrt{3}+\dfrac{6}{\sqrt{3}}=3\sqrt{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2020
4.
Ta có:
\(a^3+1+1\ge3a\) ; \(b^3+1+1\ge3b\) ; \(c^3+1+1\ge3c\)
\(\Rightarrow a^3+b^3+c^3+6\ge3\left(a+b+c\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
5.
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{c}\ge2\sqrt{\dfrac{a}{c}}\) ; \(\dfrac{a}{b}+\dfrac{c}{a}\ge2\sqrt{\dfrac{c}{b}}\) ; \(\dfrac{b}{c}+\dfrac{c}{a}\ge2\sqrt{\dfrac{b}{a}}\)
\(\Rightarrow\sqrt{\dfrac{b}{a}}+\sqrt{\dfrac{c}{b}}+\sqrt{\dfrac{a}{c}}\le\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}=1\)
