I
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dưới đây là một vài câu hỏi có thể liên quan tới câu hỏi mà bạn gửi lên. Có thể trong đó có câu trả lời mà bạn cần!
I
0
AH
Akai Haruma
Giáo viên
5 tháng 4 2021
Lời giải:
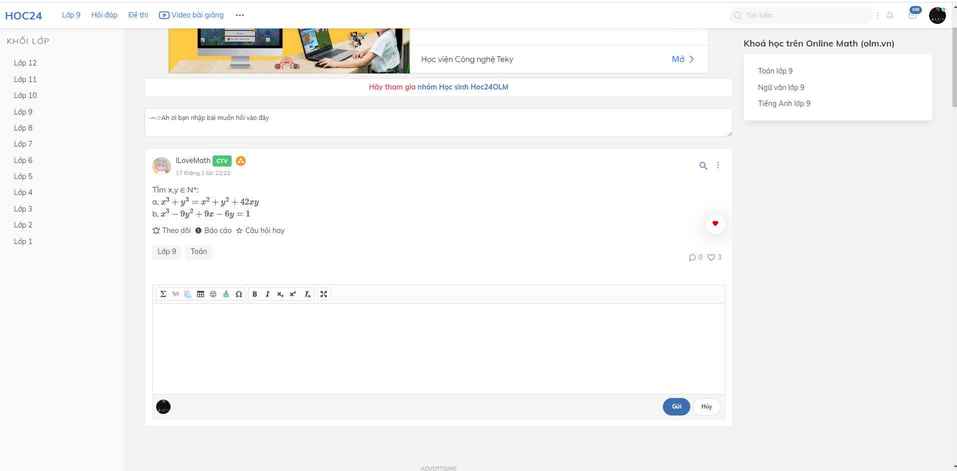
$x^3-9y^2+9x-6y=1$
$\Leftrightarrow x^3+9x=9y^2+6y+1$
$\Leftrightarrow x(x^2+9)=(3y+1)^2$
Đặt $(x,x^2+9)=d$ thì suy ra $9\vdots d(*)$
$(3y+1)^2=x(x^2+9)\vdots d^2\Rightarrow 3y+1\vdots d$. Mà $(3y+1,3)=1$ nên $(3,d)=1(**)$
Từ $(*);(**)\Rightarrow d=1$, hay $x,x^2+9$ nguyên tố cùng nhau.
$\Rightarrow \frac{x}{x^2+9}$ là phấn số tối giản.
5 tháng 7 2021
a) Ta có: \(A=3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+30\)
\(=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+30\)
\(=14\sqrt{2x}+30\)
b) Ta có: \(B=4\sqrt{\dfrac{25x}{4}}-\dfrac{8}{3}\sqrt{\dfrac{9x}{4}}-\dfrac{4}{3x}\cdot\sqrt{\dfrac{9x^3}{64}}\)
\(=4\cdot\dfrac{5\sqrt{x}}{2}-\dfrac{8}{3}\cdot\dfrac{3\sqrt{x}}{2}-\dfrac{4}{3x}\cdot\dfrac{3x\sqrt{x}}{8}\)
\(=10\sqrt{x}-4\sqrt{x}-\dfrac{1}{2}\sqrt{x}\)
\(=\dfrac{11}{2}\sqrt{x}\)
c) Ta có: \(\dfrac{y}{2}+\dfrac{3}{4}\sqrt{9y^2-6y+1}-\dfrac{3}{2}\)
\(=\dfrac{1}{2}y+\dfrac{3}{4}\left(1-3y\right)-\dfrac{3}{2}\)
\(=\dfrac{1}{2}y+\dfrac{3}{4}-\dfrac{9}{4}y-\dfrac{3}{2}\)
\(=-\dfrac{7}{4}y-\dfrac{3}{4}\)
26 tháng 9 2021
\(\left\{{}\begin{matrix}x^3-3x^2-9x+22=y^3+3y^2-9y\left(1\right)\\x^2+y^2-x+y=\dfrac{1}{2}\left(2\right)\end{matrix}\right.\)
PT (1)\(\Leftrightarrow\left(x-y\right)^3+3xy\left(x-y\right)-3\left(x^2+y^2\right)-9\left(x-y\right)=-22\)
\(\Leftrightarrow\left(x-y\right)^3+3xy\left(x-y\right)-3\left(x-y\right)^2-6xy-9\left(x-y\right)=-22\)
PT (2)\(\Leftrightarrow\left(x-y\right)^2-\left(x-y\right)+2xy=\dfrac{1}{2}\)
Đặt \(\left\{{}\begin{matrix}a=x-y\\b=xy\end{matrix}\right.\)
Hệ tt \(\left\{{}\begin{matrix}a^3+3ab-3a^2-6b-9a=-22\\a^2-a+2b=\dfrac{1}{2}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a^3+3ab-3a^2-6b-9a=-22\\b=\dfrac{1-2a^2+2a}{4}\end{matrix}\right.\)
\(\Rightarrow a^3+3a\left(\dfrac{1-2a^2+2a}{4}\right)-3a^2-6\left(\dfrac{1-2a^2+2a}{4}\right)-9a=-22\)
\(\Leftrightarrow-2a^3+6a^2-45a+82=0\)
\(\Leftrightarrow a=2\)\(\Rightarrow b=-\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x-y=2\\xy=-\dfrac{3}{4}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=-\dfrac{1}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}y=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\)
Vậy...
KN
24 tháng 5 2020
Áp dụng bất đẳng thức Cauchy-Schwarz, ta được:
\(\left(9x^3+3y^2+z\right)\left(\frac{1}{9x}+\frac{1}{3}+z\right)\ge\left(x+y+z\right)^2\)
\(\Rightarrow\frac{x}{9x^3+3y^2+z}\le\frac{x\left(\frac{1}{9x}+\frac{1}{3}+z\right)}{\left(x+y+z\right)^2}=\frac{\frac{1}{9}+\frac{x}{3}+zx}{\left(x+y+z\right)^2}\)(1)
Hoàn toàn tương tự, ta có: \(\frac{y}{9y^3+3z^2+x}\le\frac{\frac{1}{9}+\frac{y}{3}+xy}{\left(x+y+z\right)^2}\)(2); \(\frac{z}{9z^3+3x^2+y}\le\frac{\frac{1}{9}+\frac{z}{3}+yz}{\left(x+y+z\right)^2}\)(3)
Cộng theo vế của 3 bất đẳng thức (1), (2), (3), ta được:
\(\frac{x}{9x^3+3y^2+z}+\frac{y}{9y^3+3z^2+x}+\frac{z}{9z^3+3x^2+y}\)\(\le\frac{\frac{1}{9}.3+\frac{x+y+z}{3}+xy+yz+zx}{\left(x+y+z\right)^2}\)
\(\le\frac{\frac{1}{9}.3+\frac{x+y+z}{3}+\frac{\left(x+y+z\right)^2}{3}}{\left(x+y+z\right)^2}=1\)(*)
Mặt khác, có: \(2017\left(xy+yz+zx\right)\le2017.\frac{\left(x+y+z\right)^2}{3}=\frac{2017}{3}\)(**)
Từ (*) và (**) suy ra \(A=\frac{x}{9x^3+3y^2+z}+\frac{y}{9y^3+3z^2+x}+\frac{z}{9z^3+3x^2+y}+2017\left(xy+yz+zx\right)\)
\(\le1+\frac{2017}{3}=\frac{2020}{3}\)
Đẳng thức xảy ra khi \(x=y=z=\frac{1}{3}\)
YY
0
26 tháng 5 2018
Ta có:\(\left(9x^3+3y^2+z\right)\left(\dfrac{1}{9x}+\dfrac{1}{3}+z\right)\ge\left(x+y+z\right)^2\)
\(\Leftrightarrow\dfrac{x}{9x^3+3y^2+z}\le\dfrac{x\left(\dfrac{1}{9x}+\dfrac{1}{3}+z\right)}{\left(x+y+z\right)^2}=\dfrac{\dfrac{1}{9}+\dfrac{x}{3}+xz}{\left(x+y+z\right)^2}\)
Tương tự rồi cộng theo vế:
\(Σ_{cyc}\dfrac{x}{9x^3+3y^2+z}\le\dfrac{\dfrac{1}{9}\cdot3+\dfrac{x+y+z}{3}+xy+yz+xz}{\left(x+y+z\right)^2}\)
\(\le\dfrac{\dfrac{1}{9}\cdot3+\dfrac{x+y+z}{3}+\dfrac{\left(x+y+z\right)^2}{3}}{\left(x+y+z\right)^2}=1\)
Lại có: \(2017\left(xy+yz+xz\right)\le2017\dfrac{\left(x+y+z\right)^2}{3}=\dfrac{2017}{3}\)
\(\Rightarrow A\le\dfrac{2020}{3}\)
Dấu "=" khi \(x=y=z=\dfrac{1}{3}\)
Vậy ko ra yếu zzzz
Kêu lớp 8 mà đăng lớp 9 hả trời:)
học trước r