Cho tam giác DEF vuông tại D. Kẻ đường cao DH
a) Chứng minh tam giác DEF đồng dạng với tam giác HED
b) Chứng minh DH2 = HE.HF
Mình đang cần gấp mong mn giúp đợ ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔDEF vuông tại D và ΔHED vuông tại H có
góc DEF chung
Do đó:ΔDEF\(\sim\)ΔHED
b: Xét ΔDEF vuông tại D có DH là đường cao
nên \(DH^2=HE\cdot HF\)

Sửa đề: IK//DH
a: Xét ΔDEF vuông tại D và ΔHED vuông tại H có
góc E chung
=>ΔDEF đồng dạng với ΔHED
=>DF/DH=EF/DE=DE/HE
=>EH*EF=ED^2
b: Xét ΔFIK vuông tại I và ΔFDE vuông tại D có
góc F chung
=>ΔFIK đồng dạng với ΔFDE
=>FI/FD=FK/FE
=>FI*FE=FK*FD
c: góc KDE+góc KIE=180 độ
=>KDEI nội tiếp
=>góc DKE=góc DIE và góc DEK=góc DIK
mà góc DIE=góc DIK
nên góc DKE=góc DEK
=>ΔDEK cân tại D

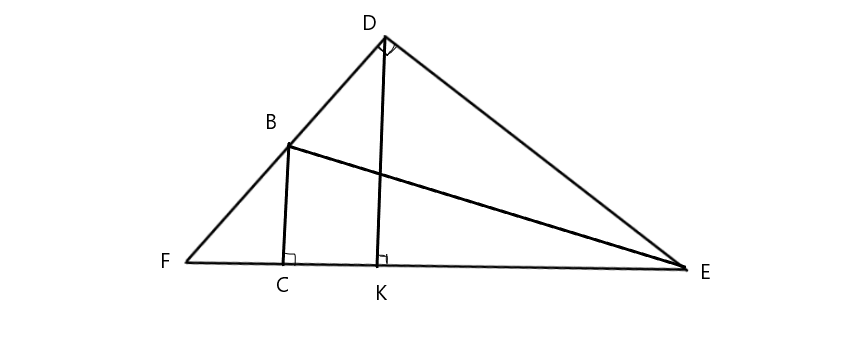
a) Xét Δ DEF vuông tại D ( gt ) có:
∠ DFE + ∠ DEF = 90o ( Tổng 2 góc nọn trong Δ vuông)
Tương tự, ta có :
∠ DFK + ∠ KDF = 90o
=> ∠ KDF = ∠ DEF
Xét Δ KDE và Δ DFE có:
∠ KDF = ∠ DEF (cmt)
∠ DKE = ∠ EDF ( = 90o )
=> Δ KDE ∞ Δ DFE
b) Tương tự, ta có
Δ KFD ∞ Δ DFE
=> Δ KFD ∞ Δ KDE
=> \(\dfrac{DK}{KE}\)= \(\dfrac{KF}{DK}\)
=> DK2 = KE.KF

a, Xét \(\Delta\)DEF và \(\Delta\)HED ta cs
^EDF = ^EHD = 900
^E - chug
=> \(\Delta\)DEF đồng dạng \(\Delta\)HED
b, Xét \(\Delta\)DEF và \(\Delta\)HDF ta cs
^EDF = ^DHF = 900
^F - chug
=> \(\Delta\)DEF đồng dạng \(\Delta\)HDF
=> \(\frac{DF}{EF}=\frac{FH}{DF}\)( đ/n )
=> DF2 = FH . EF
c, chưa nghĩ ra

a: Xét ΔDNH vuông tại N và ΔDMF vuông tại M có
góc MDF chung
=>ΔDNH đồng dạng với ΔDMF
b: Xét ΔEMH vuông tại M và ΔENF vuông tại N có
góc MEH chung
=>ΔEMH đồng dạng với ΔENF
c: Xét ΔEIH có
EM vừa là đường cao, vừa là trung tuyến
=>ΔEIH cân tại E
a. xét tam giác DEF và tam giác HED:
góc D= góc H= 90o
góc E chung
=> tam giác DEF ~ tam giác HED (g.g)
b. xét tam giác DHF và tam giác EDF:
góc D= góc H = 90o
góc F chung
=> tam giác DHF ~ tam giác EDF
=> tam giác DHF~tam giác EHD (tính chất bắc cầu)
=> \(\dfrac{DH}{HF}\)=\(\dfrac{HE}{DH}\)
vậy DH2=HE.HF