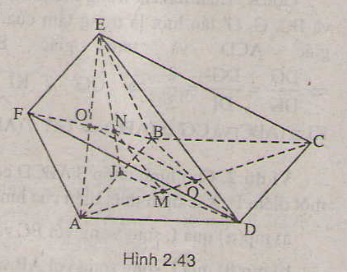
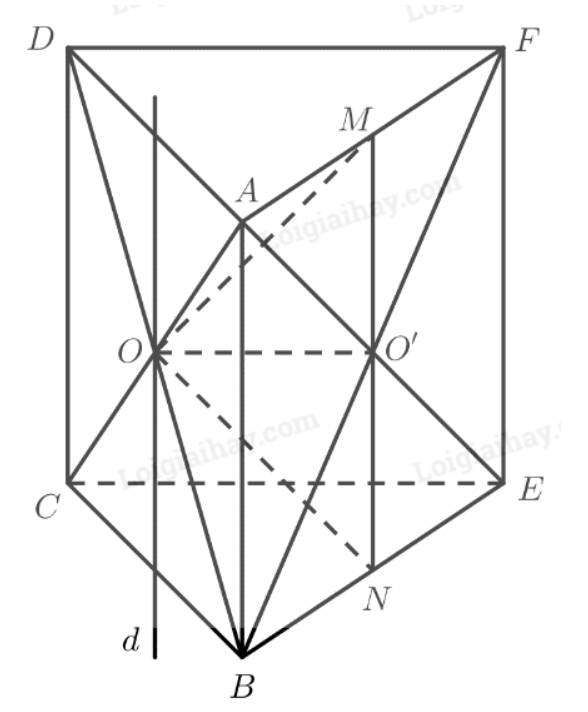
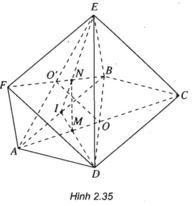
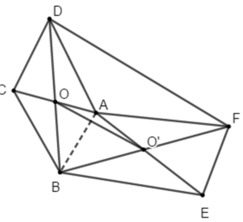
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
a) Gọi O và O’ lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thẳng OO’ song song và các mặt phẳng (ADF) và (BCF)
b) Gọi M và N lần lượt là trọng tâm của tam giác ABD và ABE. Chứng minh đường thẳng MN song song với mặt phẳng (CEF).


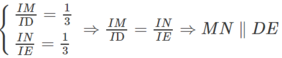
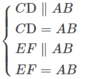
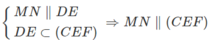

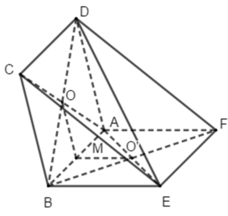
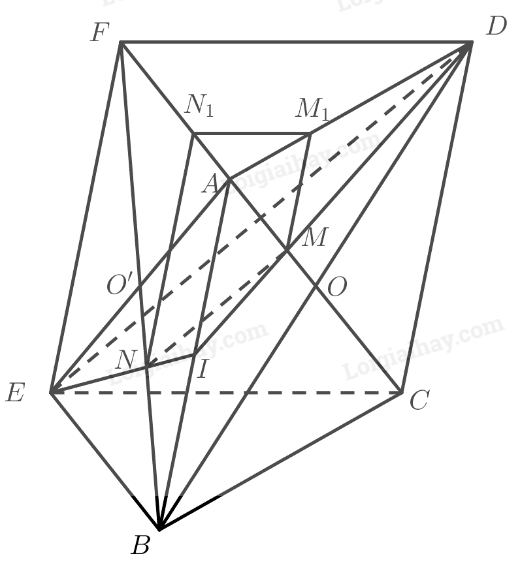
a) Do các tứ giác ABCD và ABEF là các hình bình hành
=> O là trung điểm của AC và BD
và O’ là trung điểm của AE và BF. (tính chất hình bình hành).
+ ΔBFD có OO’ là đường trung bình nên OO’ // DF
mà DF ⊂ (ADF)
⇒ OO' // (ADF)
+ ΔAEC có OO’ là đường trung bình nên OO’ // EC
mà EC ⊂ (BCE)
⇒ OO’ // (BCE).
b)
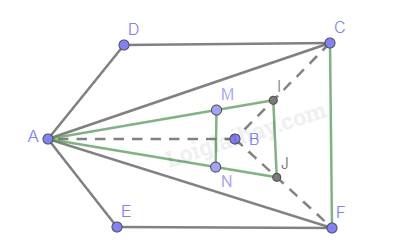
Ta thấy mp(CEF) chính là mp(CEFD).
Gọi I là trung điểm của AB:
+ M là trọng tâm ΔABD
⇒ IM/ ID = 1/3.
+ N là trọng tâm ΔABE
⇒ IN/IE = 1/3.
+ ΔIDE có IM/ID = IN/IE = 1/3
⇒ MN // DE mà ED ⊂ (CEFD)
nên MN // (CEFD) hay MN // (CEF).