Cho đa giác đều \(A_1A_2...A_{2n}\) nội tiếp đường tròn \(\left(O,R\right)\) . Biết rằng số tam giác có các đỉnh là 3 trong 2n điểm \(A_1,A_2,...,A_{2n}\) nhiều gấp 20 lần số hình chữ nhật có các đỉnh là 4 trong 2n điểm \(A_1,A_2,...,A_{2n}\) . Tìm n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 4 2016
Số tam giác là \(C_{2n}^3\). Một đa giác đều 2n đỉnh thì có n đường chéo xuyên tâm. Cứ 2 đường chéo xuyên tâm thì có một hình chữ nhật theo yêu cầu. Vậy số hình chữ nhật là \(C_n^2\).
Theo bài ta có phương trình :
\(C_{2n}^3=20C_n^2,\left(n\ge2\right)\)
\(\Leftrightarrow\frac{\left(2n\right)!}{\left(2n-3\right)!3!}=20\frac{n!}{\left(n-2\right)!2!}\)
\(\Leftrightarrow\frac{\left(2n-2\right)\left(2n-1\right)2n}{3}=20\left(n-1\right)n\)
\(\Leftrightarrow2\left(n-1\right)\left(2n-1\right)2n=60\left(n-1\right)n\)
\(\Leftrightarrow2n-1=15\), (do \(n\ge2\))
\(\Leftrightarrow n=18\)
Vậy đa giác đều có 16 cạnh, (thập lục giác đều)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
Số vecto tạo từ 2n điểm là: \(A_{2n}^2\)
Đa giác đều 2n đỉnh có n đường chéo, cứ 2 đường chéo cho ta 1 hình chữ nhật tương ứng, do đó số hình chữ nhật có đỉnh là đỉnh của đa giác đều là: \(C_n^2\)
\(\Rightarrow A_{2n}^2=9C_n^2\Leftrightarrow\dfrac{\left(2n\right)!}{\left(2n-2\right)!}=\dfrac{9.n!}{2!.\left(n-2\right)!}\)
\(\Leftrightarrow2n\left(2n-1\right)=\dfrac{9n\left(n-1\right)}{2}\)
\(\Leftrightarrow n=5\)
13 tháng 12 2020
dạ em chưa hiểu tại sao số vecto tạo từ 2n điểm và số hình chữ nhật có đỉnh là đỉnh của đa giác đều lại ra được như kia vậy ạ :(((
CM
13 tháng 3 2018
Số tam giác có các đỉnh là 3 trong 2n điểm A1;A2;…;A2n là: 
Ta thấy ứng với hai đường chéo đi qua tâm O của đa giác A1A2…A2n cho tương ứng một hình chữ nhật có 4 đỉnh là 4 điểm trong 2n điểm A1;A2;…;A2n và ngược lại mỗi hình chữ nhật như vậy sẽ cho tương ứng hai đường chéo đi qua tâm O của đa giác.
Mà số đường chéo đi qua tâm của đa giác là n nên số hình chữ nhật có đỉnh là 4 trong 2n điểm bằng 
Theo giả thiết: 
⇒n=8.
Chọn C
. Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
CM
19 tháng 9 2017
Đáp án C
Phương pháp: Số tam giác vuông bằng số đường kính của đường tròn có đầu mút là 2 đỉnh của đa giác (H) nhân với (2n – 2) tức là số đỉnh còn lại của đa giác.
Cách giải: Số phần tử của không gian mẫu: n Ω = C 2 n 3
Tam giác vuông được chọn là tam giác chứa một cạnh là đường kính của đường tròn tâm O.
Đa giác đều 2n đỉnh chứa 2n đường chéo là đường kính của đường tròn tâm O, mỗi đường kính tạo nên 2n – 2 tam giác vuông.
Do đó số tam giác vuông trong tập S là: 
Xác suất chọn một tam giác vuông trong tập S :
22 tháng 9 2023
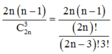
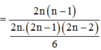
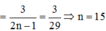
Tham khảo:
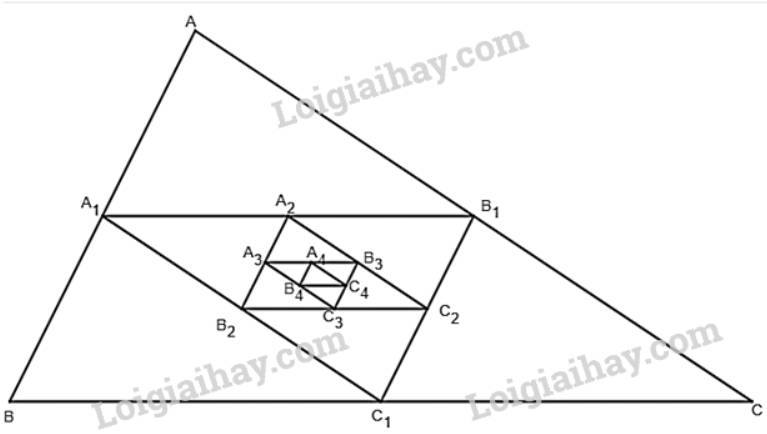
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
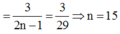
Số tam giác: \(C_{2n}^3=\frac{\left(2n\right)!}{\left(2n-3\right)!.6}=\frac{n\left(2n-1\right)\left(2n-2\right)}{3}\)
Cứ hai đường chéo qua tâm của đa giác đều sẽ đóng vai trò hai đường chéo của hình chữ nhật
Đa giác có \(n\) đường chéo qua tâm \(\Rightarrow C_n^2=\frac{n\left(n-1\right)}{2}\) hình chữ nhật
Ta có pt:
\(\frac{n\left(2n-1\right)\left(2n-2\right)}{3}=10n\left(n-1\right)\)
\(\Leftrightarrow n\left(n-1\right)\left(n-8\right)=0\Rightarrow n=8\)