Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có : \(x=9\Rightarrow\sqrt{x}=3\)
Thay vào biểu thức A ta được : \(A=\frac{2}{3-2}=2\)
b, Với \(x\ge0;x\ne4\)
\(B=\frac{\sqrt{x}}{\sqrt{x}+2}+\frac{4\sqrt{x}}{x-4}=\frac{\sqrt{x}\left(\sqrt{x}-2\right)+4\sqrt{x}}{x-4}\)
\(=\frac{x+2\sqrt{x}}{x-4}=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{x-4}=\frac{\sqrt{x}}{\sqrt{x}-2}\)( đpcm )
c, Ta có : \(A+B=\frac{3x}{\sqrt{x}-2}\)hay
\(\frac{2}{\sqrt{x}-2}+\frac{\sqrt{x}}{\sqrt{x}-2}=\frac{2+\sqrt{x}}{\sqrt{x}-2}=\frac{3x}{\sqrt{x}-2}\)
\(\Rightarrow2+\sqrt{x}=3x\Leftrightarrow3x-2-\sqrt{x}=0\)
\(\Leftrightarrow\sqrt{x}=3x-2\Leftrightarrow x=9x^2-12x+4\)
\(\Leftrightarrow\left(9x-4\right)\left(x-1\right)=0\Leftrightarrow x=\frac{4}{9}\left(ktm\right);x=1\)( đk : \(x\ge\frac{2}{3}\))

a, Ta có : \(x=4\Rightarrow\sqrt{x}=2\)
Thay vào biểu thức A ta được : \(\frac{1}{2-1}=1\)
b, Với \(x\ge0;x\ne1\)
\(Q=\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{2}{x-1}-1=\frac{\sqrt{x}\left(\sqrt{x}+1\right)-2-x+1}{x-1}\)
\(=\frac{x+\sqrt{x}-2-x+1}{x-1}=\frac{\sqrt{x}-1}{x-1}=\frac{1}{\sqrt{x}+1}\)
c, Ta có : \(\frac{1}{Q}+P\le4\)hay\(1:\frac{1}{\sqrt{x}+1}+\frac{1}{\sqrt{x}-1}\le4\)ĐK : \(x\ne1\)
\(\Leftrightarrow\frac{x-1+1}{\sqrt{x}-1}-4\le0\Leftrightarrow\frac{x-4\sqrt{x}+4}{\sqrt{x}-1}\le0\)
\(\Leftrightarrow\frac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}\le0\Rightarrow\sqrt{x}-1\le0\Leftrightarrow\sqrt{x}\le1\Leftrightarrow x\le1\)do \(\left(\sqrt{x}-2\right)^2\ge0\)
Kết hợp với đk, vậy \(x< 1\)
1, thay x=4 (TMĐKXĐ) vào P ta được:
P=\(\dfrac{1}{\sqrt{4}-1}\)=1
vậy khi x=4 thì P =1
2,với x≥0,x≠1:
Q=\(\dfrac{\sqrt{x}}{\sqrt{x}-1}\)-\(\dfrac{2}{\sqrt{x}-1}-1\)=\(\dfrac{\sqrt{x}-2-\sqrt{x}+1}{\sqrt{x}-1}\)=\(\dfrac{-1}{\sqrt{x}-1}\)
vậy Q=\(\dfrac{-1}{\sqrt{x}-1}\)
3,\(\dfrac{1}{Q}+P\le4\)
⇒1/\(\dfrac{-1}{\sqrt{x}-1}\)+\(\dfrac{1}{\sqrt{x}-1}\)≤4⇔\(\dfrac{-\sqrt{x}-1}{1}+\dfrac{1}{\sqrt{x}-1}\le4\)⇔\(\dfrac{-x+1+1}{\sqrt{x}-1}-4\le0\)⇔\(\dfrac{-x+2-4\sqrt{x}+4}{\sqrt{x}-1}\le0\)⇔\(\dfrac{-x-4\sqrt{x}+6}{\sqrt{x}-1}\le0\)⇔\(\dfrac{x+4\sqrt{x}-6}{\sqrt{x}-1}\le0\)⇔\(\dfrac{x+4\sqrt{x}+4-10}{\sqrt{x}-1}\le0\)
\(\dfrac{ \left(\sqrt{x}+2\right)^2-10}{\sqrt{x}-1}\le0\)⇒\(\sqrt{x}-1\le0\) (vì (\(\sqrt{x}+2\))\(^2\)≥0 ∀ x hay (\(\sqrt{x}+2\))\(^2\)-10>0 ∀ x)
⇔x≤1 (KTM)
vậy không có giá trị nào của x TM để \(\dfrac{1}{Q}+P\le4\)

1, Thay x = 16 vào ta được \(A=\dfrac{4}{4+3}=\dfrac{4}{7}\)
2, \(A+B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{-x+6\sqrt{x}-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}-3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{x}+3}\)
Ta có đpcm

Bài làm :
1) Khi x=9 ; giá trị của A là :
\(A=\frac{\sqrt{9}}{\sqrt{9}+2}=\frac{3}{3+2}=\frac{3}{5}\)
2) Ta có :
\(B=...\)
\(=\frac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x+2}\right)}\)
\(=\frac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}}{\sqrt{x}-2}\)
3) Ta có :
\(\frac{A}{B}=\frac{\sqrt{x}}{\sqrt{x}+2}\div\frac{\sqrt{x}}{\sqrt{x}-2}=\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\sqrt{x}}=\frac{\sqrt{x}-2}{\sqrt{x}+2}=\frac{\sqrt{x}+2-4}{\sqrt{x}+2}=1-\frac{4}{\sqrt{x}+2}\)
Xét :
\(\frac{A}{B}+1=\frac{4}{\sqrt{x+2}}>0\Rightarrow\frac{A}{B}>-1\)
=> Điều phải chứng minh
1, thay x=9(TMĐKXĐ) vào A ta đk:
A=\(\dfrac{\sqrt{9}}{\sqrt{9}-2}=3\)
vậy khi x=9 thì A =3
2,với x>0,x≠4 ta đk:
B=\(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
vậy B=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
3,\(\dfrac{A}{B}>-1\) (x>0,x≠4)
⇒\(\dfrac{\sqrt{x}}{\sqrt{x}+2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}>-1\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+2}.\dfrac{\sqrt{x}-2}{\sqrt{x}}>-1\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}+2}>-1\)
⇒\(\sqrt{x}-2>-1\) (vì \(\sqrt{x}+2>0\))
⇔\(\sqrt{x}>1\)⇔x=1 (TM)
vậy x=1 thì \(\dfrac{A}{B}>-1\) với x>0 và x≠4

a) Thay x=4 vào biểu thức \(B=\dfrac{3}{\sqrt{x}-1}\), ta được:
\(B=\dfrac{3}{\sqrt{4}-1}=\dfrac{3}{2-1}=3\)
Vậy: Khi x=4 thì B=3
b) Ta có: P=A-B
\(\Leftrightarrow P=\dfrac{6}{x-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{3}{\sqrt{x}-1}\)
\(\Leftrightarrow P=\dfrac{6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{6+x-\sqrt{x}-3\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{x-\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
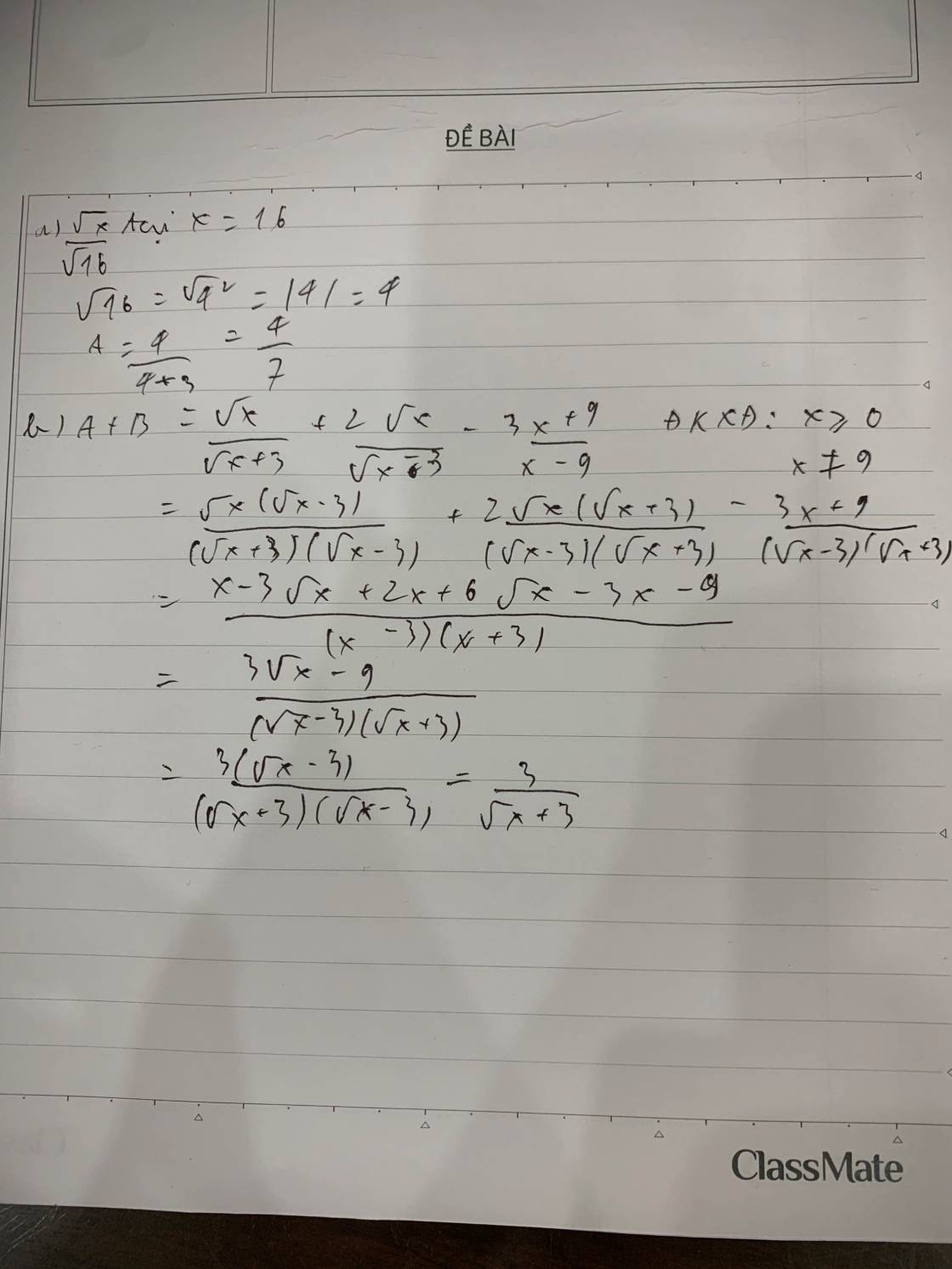
1. \(x=\frac{1}{9}\) thỏa mãn đk: \(x\ge0;x\ne9\)
Thay \(x=\frac{1}{9}\) vào A ta có:
\(A=\frac{\sqrt{\frac{1}{9}}+1}{\sqrt{\frac{1}{9}}-3}=-\frac{1}{2}\)
2. \(B=...\)
\(B=\frac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\frac{4x+6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{3x-9\sqrt{x}+x+3\sqrt{x}-4x-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
3. \(P=A:B=\frac{\sqrt{x}+1}{\sqrt{x}-3}:\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\frac{\sqrt{x}+3}{-6}\)
Vì \(\sqrt{x}+3\ge3\forall x\)\(\Rightarrow\frac{\sqrt{x}+3}{-6}\le\frac{3}{-6}=-\frac{1}{2}\)
hay \(P\le-\frac{1}{2}\)
Dấu "=" xảy ra <=> x=0
toán lớp 9 khó zậy em đọc k hỉu 1 phân số