Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Vì OA, OB, OC đôi một vuông góc với nhau 1 d 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Với d là khoảng cách từ O -> (ABC) suy ra 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức, ta có x 2 a + y 2 b + z 2 c ≥ x + y + z 2 a + b + c
Vậy d m a x = 1 3

\(\overrightarrow{AB}=\left(1-a;b;0\right);\overrightarrow{AC}=\left(1-a;0;c\right);\overrightarrow{HC}=\left(-2;-2;c-1\right);\overrightarrow{HB}=\left(-2;b-2;-1\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}.\overrightarrow{HC}=0\\\overrightarrow{AC}.\overrightarrow{HB}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-2\left(1-a\right)-2b=0\\-2\left(1-a\right)-c=0\end{matrix}\right.\) \(\Rightarrow c=2b=2\left(a-1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(bc;c\left(a-1\right);b\left(a-1\right)\right)=\left(2\left(a-1\right)^2;2\left(a-1\right)^2;\left(a-1\right)^2\right)=\left(a-1\right)^2.\left(2;2;1\right)\)
A;B;C;H đồng phẳng
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right].\overrightarrow{HB}=0\Rightarrow2.\left(-2\right)+2.\left(-2\right)+1.\left(c-1\right)=0\)
\(\Rightarrow c=9\Rightarrow b=\dfrac{9}{2}\Rightarrow a=\dfrac{11}{2}\)

\(\left(ABC\right):\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\)
\(d\left[O,\left(ABC\right)\right]=\dfrac{1}{\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}}\)
\(d_{max}\Rightarrow\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)_{min}\)
Theo cô si: \(a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}\Leftrightarrow3\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow a^2b^2c^2\le1\) \(\Leftrightarrow\dfrac{1}{a^2b^2c^2}\ge1\)
Và: \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge3\sqrt[3]{\dfrac{1}{a^2}\dfrac{1}{b^2}.\dfrac{1}{c^2}}\Leftrightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge3\)
Dấu "=" xảy ra khi \(\dfrac{1}{a^2}=\dfrac{1}{b^2}=\dfrac{1}{c^2}\Leftrightarrow a=b=c=1\)
\(\Rightarrow d_{max}=\dfrac{\sqrt{3}}{3}\)

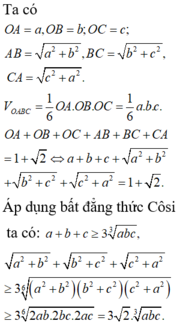
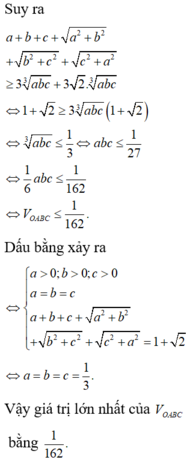

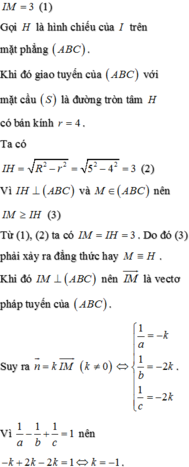
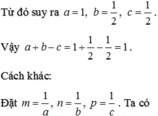

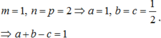
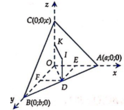

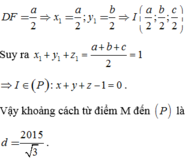
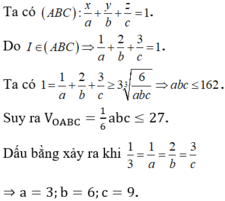


Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c khác 0
- Sử dụng bất đẳng thức
Đẳng thức xảy ra khi và chỉ khi
Cách giải:
Mặt phẳng (ABC) có phương trình:
Khoảng cách từ O đến (ABC):
Ta có
Dấu “=” xảy ra khi và chỉ khi: