Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác đều ABC có diện tích \(S = \frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Tam giác đều A'B'C' có diện tích \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích khối chóp cụt
\(V = \frac{1}{3}.HH'.\left( {S + S' + \sqrt {S.S'} } \right) = \frac{1}{3}.h.\left( {{a^2}\sqrt 3 + \frac{{{a^2}\sqrt 3 }}{4} + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} } \right) = \frac{{7{a^2}\sqrt 3 }}{{12}}\)
b) Vì ABC.A'B'C' là khối chóp cụt đều nên (ABC) // (A'B'C')
Mà \(\left( {A{B_1}{C_1}} \right) \subset \left( {ABC} \right) \Rightarrow \left( {A{B_1}{C_1}} \right)//\left( {A'B'C'} \right)\)
Xét tam giác ABC có
B1,C1 tương ứng là trung điểm của AB, AC
\( \Rightarrow \) B1C1 là đường trung bình của tam giác ABC
\( \Rightarrow \) \({B_1}{C_1} = \frac{{BC}}{2}\) và B1C1 // BC mà \(B'C' = \frac{{BC}}{2}\) và BC // B’C’
\( \Rightarrow \) B1C1 = B’C’ và B1C1 // B’C’ \( \Rightarrow \) C1C’B’B1 là hình bình hành
Ta có \(A{B_1} = A'B' = \frac{{AB}}{2},A{B_1}//A'B'\) \( \Rightarrow \) AA’B’B1 là hình bình hành.
\(A{C_1} = A'C' = \frac{{AC}}{2},A{C_1}//A'C'\) \( \Rightarrow \) AA’C’C1 là hình bình hành.
Do đó AB1C1.A'B'C' là một hình lăng trụ
Thể tích hình lăng trụ \(V = HH'.S' = h.\frac{{{a^2}\sqrt 3 }}{4}\)

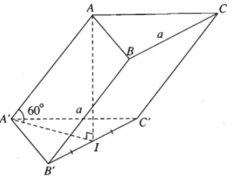
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
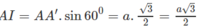
b) 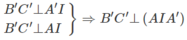
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.

Từ giả thiết suy ra với mọi O đều có ?
\(\overrightarrow{OG}=\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)\) và \(\overrightarrow{OG_1}=\frac{1}{3}\left(\overrightarrow{OA}_1+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\)
Mà :
\(\overrightarrow{OG_2=}\frac{1}{3}.\left(\overrightarrow{OGa}+\overrightarrow{OG_b}+\overrightarrow{OG_c}\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB_1}+\overrightarrow{OC_1}\right)+\frac{1}{3}\left(\overrightarrow{OB}+\overrightarrow{OC_1}+\overrightarrow{OA_1}\right)+\frac{1}{3}\left(\overrightarrow{OC}+\overrightarrow{OA_1}+\overrightarrow{OB_1}\right)\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)+\frac{2}{3}\left(\overrightarrow{OA_1}+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\right)\)
\(=\frac{1}{3}\overrightarrow{OG}+\frac{2}{3}\overrightarrow{OG_1}\)
Suy ra :
\(3\overrightarrow{OG_2}=\overrightarrow{OG}+2\overrightarrow{OG_1}\) với mọi O. Điều này có nghĩa là \(G,G_1,G_2\) thẳng hàng => Điều phải chứng minh
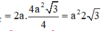
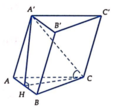
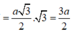
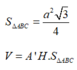
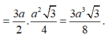
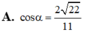
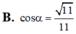
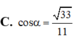
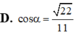
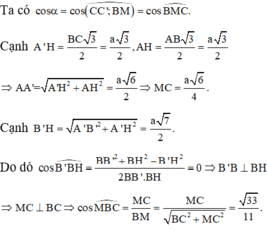
\(2x\left(y-x\right)=a^2>0\Rightarrow y>x\)
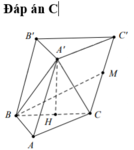
Qua \(B_1\) kẻ đường thẳng song song BC cắt \(CC'\) tại D \(\Rightarrow DC_1=y-x\) và \(B_1D=BC=a\)
Áp dụng Pitago ta có:
\(AC_1^2=AC^2+AC_1^2=a^2+y^2\)
\(AB_1^2=AB^2+BB_1^2=a^2+x^2\)
\(B_1C_1^2=B_1D^2+DC_1^2=a^2+\left(y-x\right)^2\)
\(\Rightarrow AB_1^2+B_1C_1^2=2a^2+x^2+\left(y-x\right)^2=2a^2+2x^2+y^2-2xy\)
\(=2a^2+2x^2+y^2-\left(2x^2+a^2\right)=a^2+y^2=AC_1^2\)
\(\Rightarrow\Delta AB_1C_1\) vuông tại \(B_1\) theo Pitago đảo.
b.
Do \(B_1\) là trung điểm BB' \(\Rightarrow x=\dfrac{BB'}{2}\), mà \(y=2x\Rightarrow y=BB'\Rightarrow C_1\) trùng C'
Do \(CC',B_1B\) vuông góc mặt đáy \(\Rightarrow\) tam giác ABC là hình chiếu vuông góc của tam giác \(AB_1C_1\) lên (ABC)
Theo công thức diện tích hình chiếu:
\(S_{ABC}=S_{AB_1C_1}.cos\alpha\Rightarrow S_{AB_1C_1}=\dfrac{S_{ABC}}{cos\alpha}=\dfrac{a^2\sqrt{3}}{4cos\alpha}\)
Gọi D là trung điểm AC' (hay \(AC_1\)) và E là trung điểm AC
\(\Rightarrow\) \(BEDB_1\) là hình chữ nhật \(\Rightarrow B_1D=BE=\dfrac{a\sqrt{3}}{2}\)
\(B_1C'=B_1A=\sqrt{a^2+\left(\dfrac{x}{2}\right)^2}\) nên tam giác \(AB_1C'\) cân tại \(B_1\Rightarrow B_1D\) đồng thời là đường cao
\(\Rightarrow S_{AB_1C_1}=\dfrac{1}{2}B_1D.AC'=\dfrac{a^2\sqrt{3}}{4cos\alpha}\Rightarrow AC'=\dfrac{a^2\sqrt{3}}{2cos\alpha.B_1D}=\dfrac{a}{cos\alpha}\)
\(\Rightarrow AA'=\sqrt{AC'^2-AC^2}=\sqrt{\dfrac{a^2}{cos^2\alpha}-a^2}=a.tan\alpha\)