Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

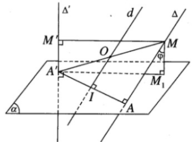
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

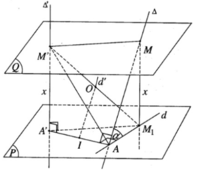
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.

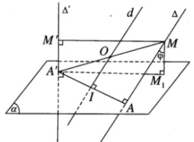
Theo giả thiết ta có: ∠A′M′M = ∠A′AM = ∠A′M1M = 90o
Do đó 5 điểm A, A’, M, M’, M1 cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính r = A′M2
Mặt khác ta có A’M2 = A’A2 + AM2
Trong đó
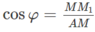
Do đó
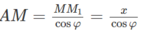
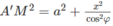
Mặt cầu tâm O có bán kính
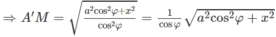
Diện tích của mặt cầu tâm O là:
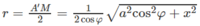

Ta chọn hệ toạ độ Oxyz có gốc là đỉnh A, tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA’ (h.105).

Khi đó :
a) Ta có
Gọi là góc giữa hai đường thẳng và ta có :
b) Ta có : ,
Vậy
QUẢNG CÁOc) Mặt phẳng song song với trục Oy nên có phương trình :
Vì mặt phẳng này đi qua nên ta xác định được p = q và n = -pa.
Cho p = 1, ta được phương trình mp là . Vectơ pháp tuyến của mặt phẳng này là
Từ giả thiết , ta tính được :
Suy ra
Ta có
Rõ ràng Suy ra MN song song với mp
d) Ta có
nhỏ nhất bằng khi (thoả mãn điều kiện ).
Vậy MN ngắn nhất bằng khi .
e) Khi MN ngắn nhất thì Khi đó
Ta lại có nên
Vậy MN là đường vuông góc chung của AD’ và DB.
Ta chọn hệ toạ độ Oxyz có gốc là đỉnh A, tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA’ (h.105).

Khi đó :
A=(0;0;0)B=(a;0;0)D=(0;a;0)C=(a;a;0)A=(0;0;0)B=(a;0;0)D=(0;a;0)C=(a;a;0) A′=(0;0;a)B′=(a;0;a)D′=(0;a;a)C′=(a;a;a)A′=(0;0;a)B′=(a;0;a)D′=(0;a;a)C′=(a;a;a)
P=(a;a2;a)P=(a;a2;a)
a) Ta có −−→AP=(a;a2;a)AP→=(a;a2;a)
−−→BC′=(0;a;a).BC′→=(0;a;a).
Gọi αα là góc giữa hai đường thẳng APAP và BC′BC′ ta có :
cosα=∣∣0+a22+a2∣∣√a2+a22+a2.√a2+a2=1√2⇒α=45ocosα=|0+a22+a2|a2+a22+a2.a2+a2=12⇒α=45o
b) Ta có : −−→AP=(a;a2;a)AP→=(a;a2;a), −−→AB=(a;0;0),−−→AC′=(a;a;a)AB→=(a;0;0),AC′→=(a;a;a)
⇒[−−→AP,−−→AB]=(∣∣∣a2a00∣∣∣;∣∣∣aa0a∣∣∣;∣∣∣aa2a0∣∣∣)=(0;a2;–a22)⇒[−−→AP,−−→AB].−−→AC′=0+a3–a32=a32.⇒[AP→,AB→]=(|a2a00|;|aa0a|;|aa2a0|)=(0;a2;–a22)⇒[AP→,AB→].AC′→=0+a3–a32=a32.
Vậy VAPBC′=16∣∣∣[−−→AP,−−→AB].−−→AC′∣∣∣=16.a32=a312.VAPBC′=16|[AP→,AB→].AC′→|=16.a32=a312.
QUẢNG CÁO
c) Mặt phẳng (A′D′CB)(A′D′CB) song song với trục Oy nên có phương trình :
px+qz+n=0px+qz+n=0 (n≠0,p2+q2>0).(n≠0,p2+q2>0).
Vì mặt phẳng này đi qua A′,B,CA′,B,C nên ta xác định được p = q và n = -pa.
Cho p = 1, ta được phương trình mp(A′D′CB)(A′D′CB) là x+z–a=0x+z–a=0. Vectơ pháp tuyến của mặt phẳng này là →n=(1;0;1).n→=(1;0;1).
Từ giả thiết M∈AD′,N∈DB;AM=DN=kM∈AD′,N∈DB;AM=DN=k, ta tính được :
M=(0;k√2;k√2),N=(k√2;a√2−k√2;0).M=(0;k2;k2),N=(k2;a2−k2;0).
Suy ra −−−→MN=(k√2;a√2−2k√2;–k√2).MN→=(k2;a2−2k2;–k2).
Ta có −−−→MN.→n=1.k√2+0(a√2−2k√2)+1.(–k√2)=0MN→.n→=1.k2+0(a2−2k2)+1.(–k2)=0
⇒−−−→MN⊥→n.⇒MN→⊥n→.
Rõ ràng N∉mp(A′D′CB).N∉mp(A′D′CB). Suy ra MN song song với mp(A′D′CB).(A′D′CB).
d) Ta có MN2=(k√2)2+(a√2−2k√2)2+(–k√2)2.MN2=(k2)2+(a2−2k2)2+(–k2)2.
=3k2–2a√2k+a2=3⎡⎣(k–a√23)2+a29⎤⎦≥3a29=a23.=3k2–2a2k+a2=3[(k–a23)2+a29]≥3a29=a23.
MN2MN2 nhỏ nhất bằng a23a23 khi k=a√23k=a23 (thoả mãn điều kiện 0<k<a√20<k<a2 ).
Vậy MN ngắn nhất bằng a√33a33 khi k=a√23k=a23.
e) Khi MN ngắn nhất thì k=a√23k=a23 Khi đó −−−→MN=(a3;a3;–a3).MN→=(a3;a3;–a3).
Ta lại có −−→AD′=(0;a;a),−−→DB=(a;–a;0)AD′→=(0;a;a),DB→=(a;–a;0) nên −−−→MN.−−→AD′=0,−−−→MN.−−→DB=0.MN→.AD′→=0,MN→.DB→=0.
Vậy MN là đường vuông góc chung của AD’ và DB.
Mặt khác −−→A′C=(a;a;–a)=3−−−→MNA′C→=(a;a;–a)=3MN→, chứng tỏ −−−→MNMN→, −−→A′CA′C→ cùng phương. Do N∉A′CN∉A′C nên MN//A′C.Ta chọn hệ toạ độ Oxyz có gốc là đỉnh A, tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA’ (h.105).

Khi đó :
A=(0;0;0)B=(a;0;0)D=(0;a;0)C=(a;a;0)A=(0;0;0)B=(a;0;0)D=(0;a;0)C=(a;a;0) A′=(0;0;a)B′=(a;0;a)D′=(0;a;a)C′=(a;a;a)A′=(0;0;a)B′=(a;0;a)D′=(0;a;a)C′=(a;a;a)
P=(a;a2;a)P=(a;a2;a)
a) Ta có −−→AP=(a;a2;a)AP→=(a;a2;a)
−−→BC′=(0;a;a).BC′→=(0;a;a).
Gọi αα là góc giữa hai đường thẳng APAP và BC′BC′ ta có :
cosα=∣∣0+a22+a2∣∣√a2+a22+a2.√a2+a2=1√2⇒α=45ocosα=|0+a22+a2|a2+a22+a2.a2+a2=12⇒α=45o
b) Ta có : −−→AP=(a;a2;a)AP→=(a;a2;a), −−→AB=(a;0;0),−−→AC′=(a;a;a)AB→=(a;0;0),AC′→=(a;a;a)
⇒[−−→AP,−−→AB]=(∣∣∣a2a00∣∣∣;∣∣∣aa0a∣∣∣;∣∣∣aa2a0∣∣∣)=(0;a2;–a22)⇒[−−→AP,−−→AB].−−→AC′=0+a3–a32=a32.⇒[AP→,AB→]=(|a2a00|;|aa0a|;|aa2a0|)=(0;a2;–a22)⇒[AP→,AB→].AC′→=0+a3–a32=a32.
Vậy VAPBC′=16∣∣∣[−−→AP,−−→AB].−−→AC′∣∣∣=16.a32=a312.VAPBC′=16|[AP→,AB→].AC′→|=16.a32=a312.
QUẢNG CÁO
c) Mặt phẳng (A′D′CB)(A′D′CB) song song với trục Oy nên có phương trình :
px+qz+n=0px+qz+n=0 (n≠0,p2+q2>0).(n≠0,p2+q2>0).
Vì mặt phẳng này đi qua A′,B,CA′,B,C nên ta xác định được p = q và n = -pa.
Cho p = 1, ta được phương trình mp(A′D′CB)(A′D′CB) là x+z–a=0x+z–a=0. Vectơ pháp tuyến của mặt phẳng này là →n=(1;0;1).n→=(1;0;1).
Từ giả thiết M∈AD′,N∈DB;AM=DN=kM∈AD′,N∈DB;AM=DN=k, ta tính được :
M=(0;k√2;k√2),N=(k√2;a√2−k√2;0).M=(0;k2;k2),N=(k2;a2−k2;0).
Suy ra −−−→MN=(k√2;a√2−2k√2;–k√2).MN→=(k2;a2−2k2;–k2).
Ta có −−−→MN.→n=1.k√2+0(a√2−2k√2)+1.(–k√2)=0MN→.n→=1.k2+0(a2−2k2)+1.(–k2)=0
⇒−−−→MN⊥→n.⇒MN→⊥n→.
Rõ ràng N∉mp(A′D′CB).N∉mp(A′D′CB). Suy ra MN song song với mp(A′D′CB).(A′D′CB).
d) Ta có MN2=(k√2)2+(a√2−2k√2)2+(–k√2)2.MN2=(k2)2+(a2−2k2)2+(–k2)2.
=3k2–2a√2k+a2=3⎡⎣(k–a√23)2+a29⎤⎦≥3a29=a23.=3k2–2a2k+a2=3[(k–a23)2+a29]≥3a29=a23.
MN2MN2 nhỏ nhất bằng a23a23 khi k=a√23k=a23 (thoả mãn điều kiện 0<k<a√20<k<a2 ).
Vậy MN ngắn nhất bằng a√33a33 khi k=a√23k=a23.
e) Khi MN ngắn nhất thì k=a√23k=a23 Khi đó −−−→MN=(a3;a3;–a3).MN→=(a3;a3;–a3).
Ta lại có −−→AD′=(0;a;a),−−→DB=(a;–a;0)AD′→=(0;a;a),DB→=(a;–a;0) nên −−−→MN.−−→AD′=0,−−−→MN.−−→DB=0.MN→.AD′→=0,MN→.DB→=0.
Vậy MN là đường vuông góc chung của AD’ và DB.
Mặt khác −−→A′C=(a;a;–a)=3−−−→MNA′C→=(a;a;–a)=3MN→, chứng tỏ −−−→MNMN→, −−→A′CA′C→ cùng phương. Do N∉A′CN∉A′C nên MN//A′C.
Mặt khác , chứng tỏ , cùng phương. Do nên

Khi đó :
a) Ta có
Gọi là góc giữa hai đường thẳng và ta có :
b) Ta có : ,
Vậy
QUẢNG CÁOc) Mặt phẳng song song với trục Oy nên có phương trình :
Vì mặt phẳng này đi qua nên ta xác định được p = q và n = -pa.
Cho p = 1, ta được phương trình mp là . Vectơ pháp tuyến của mặt phẳng này là
Từ giả thiết , ta tính được :
Suy ra
Ta có
Rõ ràng Suy ra MN song song với mp
d) Ta có
nhỏ nhất bằng khi (thoả mãn điều kiện ).
Vậy MN ngắn nhất bằng khi .
e) Khi MN ngắn nhất thì Khi đó
Ta lại có nên
Vậy MN là đường vuông góc chung của AD’ và DB.
Mặt khác , chứng tỏ , cùng phương. Do nên

Đáp án D.
Do AB//Ox => A, B nằm trên đường thẳng y = m ( m ≠ 0 )
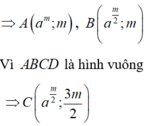
Do SABCD = 36
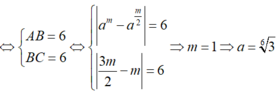 .
.
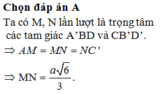
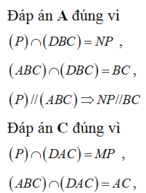


Chọn B
* Sử dụng định lí Ta-lét đảo.
Ta có: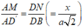
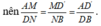
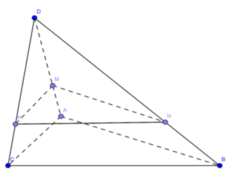
Áp dụng định lí Ta-lét đảo, ta có AD, MN, BD' lần lượt nằm trên ba mặt phẳng song song.
=> M song song với mặt phẳng (P) chứa BD' và song song với AD.
Nên MN//(BCD'A') hay MN//(A'BC)
* Sử dụng định lí Ta-lét.
* Sử dụng định lí Ta-lét.
Vì AD//A'D' nên tồn tại (P) là mặt phẳng qua AD và song song với mp (A'D'CB)
(Q) là mặt phẳng qua M và song song với mp (A'D'CB). Giả sử (Q) cắt DB tại N
Theo định lí Ta-lét ta có: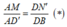
Mà các mặt của hình hộp là hình vuông cạnh a nên AD' = DB = a 2
Từ (*), ta có: AM = DN' => DN' = DN
(Q)//(A'D'CB) suy ra luôn song song với mặt phẳng cố định (A'D'CB) hay (A'BC)