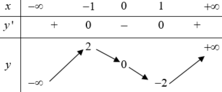
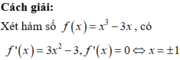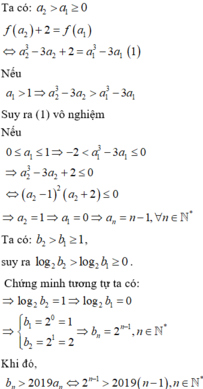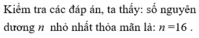Cho các số a,b dương thỏa mãn căn bậc N của (a1+b1)(a2+b2).....(an+bn) lớn hơn hoặc bằng căn bậc N của a1a2....an cộng căn bậc n của b1b2....b3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 7 2021
Bài 1:
Uses crt;
var i,n,j:integer;
a,b,c:array[1..100000] of integer;
Begin
clrscr;
readln(n);
for i:= 1 to n do readln(a[i]);
for i:= 1 to n do readln(b[i]);
j:=0;
for i:= 1 to n do
Begin
inc(j);
c[j] := a[i];
inc(j);
c[j] := b[i];
end;
for i:= 1 to j do write(c[i],' ');
readln;
end.
TT
6 tháng 8 2020
Áp dụng bất đẳng thức Cosi, ta có:
\(\left(a^2+b+c\right)\left(1+b+c\right)\ge\left(a+b+c\right)^2\)Do đó, để chứng minh bất đẳng thức đã cho, ta chỉ cần chứng minh rằng:
\(\frac{a\sqrt{1+b+c}+b\sqrt{1+c+a}+c\sqrt{1+a+b}}{a+b+c}\le\sqrt{3}\)
Áp dụng bất đẳng thức Côsi lần thứ hai ta nhận được:
\(VT=\frac{\sqrt{a}\sqrt{a\left(1+b+c\right)}+\sqrt{b}\sqrt{b\left(1+c+a\right)}+\sqrt{c}\sqrt{c\left(1+a+b\right)}}{a+b+c}\)
\(\le\frac{\sqrt{\left(a+b+c\right)\left[a\left(1+b+c\right)+b\left(1+c+a\right)+c\left(1+a+b\right)\right]}}{a+b+c}\)
\(=\sqrt{1+\frac{2\left(ab+bc+ca\right)}{a+b+c}}\)
\(\le\sqrt{1+\frac{2\left(a+b+c\right)}{3}}\)
\(\le\sqrt{1+\frac{2\sqrt{3\left(a^2+b^2+c^2\right)}}{3}}=\sqrt{3}\left(đpcm\right)\)
Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.
AH
Akai Haruma
Giáo viên
8 tháng 7 2017
Lời giải:
Áp dụng BĐT AM-GM có:
\(\sqrt[3]{a+b}=\sqrt[3]{\frac{9}{4}}\sqrt[3]{(a+b).\frac{4}{9}}\leq \sqrt[3]{\frac{9}{4}}\left ( \frac{a+b+\frac{2}{3}+\frac{2}{3}}{3} \right )\)
Thực hiện tương tự với các biểu thức còn lại và cộng theo vế:
\(\Rightarrow A\leq \sqrt[3]{\frac{9}{4}}\left [ \frac{2(a+b+c)+4}{3} \right ]=2\sqrt[3]{\frac{9}{4}}\)
Vậy \(A_{\max}=2\sqrt[3]{\frac{9}{4}}\Leftrightarrow a=b=c=\frac{1}{3}\)
HD
0
