VP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VP
0
CM
4 tháng 10 2018
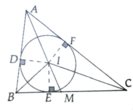
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b
30 tháng 8 2017
Do a,b,c là 3 cạnh tam giác nên \(a+b-c>0;b+c-a>0;c+a-b>0\)
Đặt \(x=b+c-a>0\)
\(y=a+c-b>0\)
\(z=a+b-c>0\)
\(\Rightarrow a=\frac{"y+z"}{2}\)
\(\Rightarrow b=\frac{"x+z"}{2}\)
\(\Rightarrow c=\frac{"x+y"}{2}\)
\(A=\frac{a}{"b+c-a"}+\frac{b}{"a+c-b"}+\frac{c}{"a+b-c"}\)
\(=\frac{"y+z"}{"2x"}+\frac{"x+z"}{"2y"}+\frac{"x+y"}{"2z"}\)
\(=\frac{1}{2}."\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}"\)
Áp dụng công thức bdt Cauchy cho 2 số :
\(\frac{x}{y}+\frac{y}{x}\ge2\)
\(\frac{x}{z}+\frac{z}{x}\ge2\)
\(\frac{y}{z}+\frac{z}{y}\ge2\)
Cộng 3 bdt trên, suy ra :
\("\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}"\ge6\)
\(\Rightarrow A\ge\frac{1}{2}.6=3\) "dpcm"
P/s: Nhớ thay thế dấu ngoặc kép thành dấu ngoặc đơn nhé
30 tháng 11 2019
\(\hept{\begin{cases}\frac{ab}{c}+\frac{bc}{a}\ge2b\\\frac{bc}{a}+\frac{ca}{b}\ge2c\\\frac{ca}{b}+\frac{ab}{c}\ge2a\end{cases}}\) :)))
8 tháng 7 2023
BĐT\(\Leftrightarrow\dfrac{a}{-a+b+c}+\dfrac{b}{a-b+c}+\dfrac{c}{a+b-c}\ge3\)
Áp dụng BĐT Svac-xơ, ta có:
\(\dfrac{a^2}{-a^2+ab+ac}+\dfrac{b^2}{ab-b^2+bc}+\dfrac{c^2}{ac+bc-c^2}\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)-\left(a^2+b^2+c^2\right)}\)
Ta có: \(a,b,c\) là 3 cạnh của 1 tam giác nên:
\(a\left(b+c\right)>a^2\). Tương tự và cộng theo vế, ta có:
\(2\left(ab+bc+ca\right)-\left(a^2+b^2+c^2\right)>0\)
Ta sẽ chứng minh \(\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)-\left(a^2+b^2+c^2\right)}\ge3\left(1\right)\)
Thật vậy, \(BĐT\left(1\right)\Leftrightarrow3\left(a^2+b^2+c^2\right)+\left(a+b+c\right)^2\ge6\left(ab+bc+ca\right)\), đúng
Đẳng thức xảy ra khi và chỉ khi \(a=b=c\)
8 tháng 7 2023
Cách 2:
Đặt \(\left\{{}\begin{matrix}-a+b+c=x\\a-b+c=y\\a+b-c=z\end{matrix}\right.\) với \(x,y,z>0\)
Khi đó ta có \(a=\dfrac{y+z}{2};b=\dfrac{x+z}{2};c=\dfrac{x+y}{2}\)
BĐT cần chứng minh trở thành:
\(\dfrac{y+z}{x}+\dfrac{x+z}{y}+\dfrac{x+y}{z}\ge6\), đúng theo bđt Cauchy
Đẳng thức xảy ra khi và chỉ khi \(x=y=z\Leftrightarrow a=b=c\)
ML
20 tháng 11 2015
\(\Leftrightarrow2\left(p-a\right).2\left(p-b\right).2\left(p-c\right)\le abc\)
\(\Leftrightarrow\left(2p-2a\right)\left(2p-2b\right)\left(2p-2c\right)\le abc\)
\(\Leftrightarrow\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)\le abc\)
Đặt \(a+b-c=x;\text{ }b+c-a=y;\text{ }c+a-b=z\)
Thì \(a=\frac{x+z}{2};\text{ }b=\frac{y+x}{2};\text{ }c=\frac{z+y}{2}\)
Nên cần chứng minh:
\(xyz\le\frac{1}{8}\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
Điều này là hiển nhiên khi ta áp dụng bđt Côsi cho VP.
Vậy ta có đpcm.
NT
5 tháng 2 2016
\(\cfrac{P}{P-a}=\cfrac{2P}{2P-2a}=\cfrac{2P}{a+b+b-2a}=\cfrac{2P}{-a+b+c}\)
Chứng minh tương tự => \(\cfrac{P}{P-b}=\cfrac{2P}{a-b+c} \); \(\cfrac{P}{P-c}=\cfrac{2P}{a+b-c}\)
=>VT=\(\cfrac{2P}{-a+b+c}+\cfrac{2P}{a-b+c}+\cfrac{2P}{a+b-c} \geq 2P\cfrac{(1+1+1)^2}{a+b +c}=9\)(Áp dụng bđt \(\cfrac{a^2}{x}+\cfrac{b^2}{y}+\cfrac{c^c}{z}\geq\cfrac{(a+b+c)^2}{x+y+z}\))
Đặt \(S=\frac{ab}{p-c}+\frac{bc}{p-a}+\frac{ca}{p-b}\)
Bất đẳng thức cần chứng minh tương đương với \(S=\frac{2ab}{a+b-c}+\frac{2bc}{b+c-a}+\frac{2ca}{c+a-b}\ge2\left(a+b+c\right)\)
Đặt \(a+b-c=x;b+c-a=y;c+a-b=z\)thì \(x+y+z=a+b+c;a=\frac{y+z}{2};b=\frac{z+x}{x};c=\frac{x+y}{2}\)
Ta cần chứng minh \(S=\text{∑}_{cyc}\frac{\left(y+z\right)\left(z+x\right)}{2z}\ge2\left(x+y+z\right)\)
Ta có:
\(S=\frac{\left(y+z\right)\left(z+x\right)}{2z}+\frac{\left(x+y\right)\left(y+z\right)}{2y}+\frac{\left(z+x\right)\left(x+y\right)}{2x}\)
\(=\frac{xy+yz+zx+z^2}{2z}+\frac{xy+zx+yz+y^2}{2y}+\frac{x^2+xy+zx+yz}{2x}\)