`#3107.101107`

`a)`

- Tổng của 2 số hữu tỉ khác dấu: \(-\dfrac{4}{15}=-\dfrac{13}{15}+\dfrac{9}{15}\)

`b)`

- Tích cảu 2 số hữu tỉ: \(-\dfrac{4}{15}=-\dfrac{8}{15}\cdot\dfrac{1}{2}\)

`c)`

Thương của 2 số hữu tỉ: \(-\dfrac{4}{15}=-\dfrac{16}{15}\div2\)

a; \(\dfrac{98}{99}\) > \(\dfrac{98}{100}\) (hai phân số dương có cùng tử số, phân số nào có mẫu lớn hơn thì phân số đó lớn hơn)

   \(\dfrac{98}{100}\) > \(\dfrac{97}{100}\)(hai phân số dương có cùng mẫu số, phân số nào có tử số lớn hơn thì phân số đó lớn hơn)

Vậy  \(\dfrac{97}{100}\)  < \(\dfrac{98}{99}\)

b;   \(\dfrac{19}{18}\) = 1 + \(\dfrac{1}{18}\)

     \(\dfrac{2021}{2020}\) = 1 + \(\dfrac{1}{2020}\)

      \(\dfrac{1}{18}\) > \(\dfrac{1}{2020}\)  (hai phân số dương có cùng tử số phân số nào có mẫu số nhỏ hơn thì phân số đó lớn hơn)

     \(\dfrac{19}{18}\) > \(\dfrac{2021}{2020}\) (hai phân số phân số nào có phần hơn lớn hơn thì phân số đó lớn hơn)

Vậy: \(\dfrac{19}{18}\) > \(\dfrac{2021}{2020}\)

a) \(\dfrac{2x+1}{9}=\dfrac{5}{x+1}\left(x\ne-1\right)\)

\(\Rightarrow\left(2x+1\right)\left(x+1\right)=9\cdot5=45\)

\(\Rightarrow2x^2+2x+x+1=45\)

\(\Rightarrow2x^2+3x-44=0\)

\(\Rightarrow2x^2+11x-8x-44=0\)

\(\Rightarrow x\left(2x+11\right)-4\left(2x+11\right)=0\)

\(\Rightarrow\left(x-4\right)\left(2x+11\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=4\\2x=-11\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{11}{2}\end{matrix}\right.\)

b) \(\dfrac{2x-1}{21}=\dfrac{3}{2x+1}\left(x\ne-\dfrac{1}{2}\right)\)

\(\Rightarrow\left(2x-1\right)\left(2x+1\right)=21\cdot3=63\)

\(\Rightarrow4x^2-1=63\)

\(\Rightarrow4x^2=64\)

\(\Rightarrow\left(2x\right)^2=8^2\)

\(\Rightarrow\left[{}\begin{matrix}2x=8\\2x=-8\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

c) \(\dfrac{2x-1}{2}=\dfrac{5}{x}\left(x\ne0\right)\)

\(\Rightarrow x\left(2x-1\right)=5\cdot2=10\)

\(\Rightarrow2x^2-x=10\)

\(\Rightarrow2x^2-x-10=0\)

\(\Rightarrow2x^2+4x-5x-10=0\)

\(\Rightarrow2x\left(x+2\right)-5\left(x+2\right)=0\)

\(\Rightarrow\left(2x-5\right)\left(x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}2x=5\\x=-2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\end{matrix}\right.\)

d) \(\dfrac{x-3}{3}=\dfrac{2x+1}{5}\)

\(\Rightarrow15\cdot\dfrac{x-3}{3}=15\cdot\dfrac{2x+1}{5}\)

\(\Rightarrow5\left(x-3\right)=3\left(2x+1\right)\)

\(\Rightarrow5x-15=6x+3\)

\(\Rightarrow6x-5x=-18\)

\(\Rightarrow x=-18\)

Sửa đề:

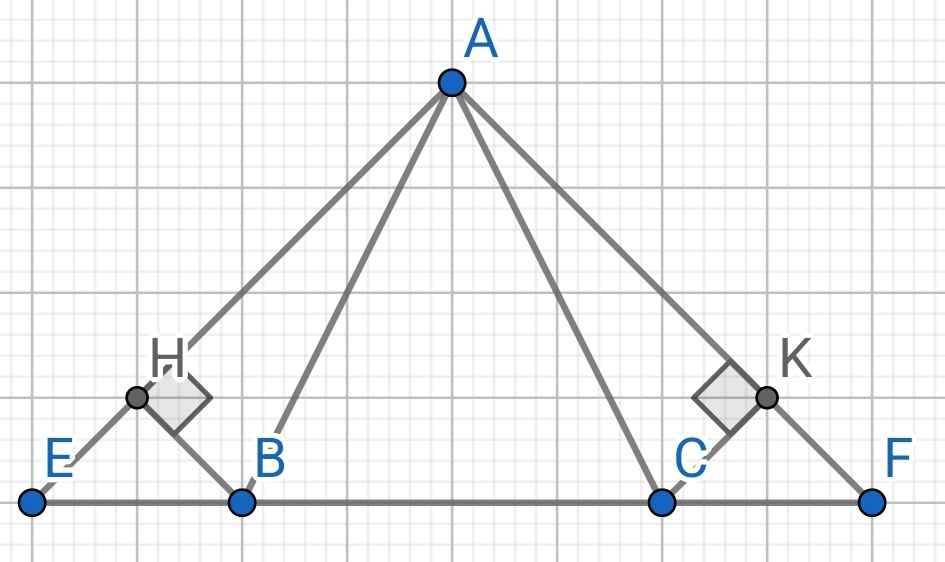
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF

a) Chứng minh tam giác  AEF cân

b) vẽ BH vuông góc AE, CK vuông góc AF. CM tam giác EBH bằng tam giác FCK.

Giải

a) Do ∆ABC cân tại A (gt)

⇒ AB = AC và ∠ABC = ∠ACB

Ta có:

∠ABC + ∠ABE = 180⁰ (kề bù)

∠ACB + ∠ACF = 180⁰ (kề bù)

Mà ∠ABC = ∠ACB (cmt)

⇒ ∠ABE = ∠ACF

Xét ∆ABE và ∆ACF có:

AB = AC (cmt)

∠ABE = ∠ACF (cmt)

BE = CF (gt)

⇒ ∆ABE = ∆ACF (c-g-c)

⇒ AE = AF (hai cạnh tương ứng)

⇒ ∆AEF cân tại A

b) Do ∆AEF cân tại A (cmt)

⇒ ∠AEF = ∠AFE

⇒ ∠HEB = ∠KFC

Xét hai tam giác vuông: ∆EBH và ∆FCK có:

BE = CF (gt)

∠HEB = ∠KFC (cmt)

⇒ ∆EBH = ∆FCK (cạnh huyền - góc nhọn)

\(0,75+\dfrac{3}{6}-\dfrac{8}{2}=\dfrac{5}{3}+x.\dfrac{-5}{6}\\ \Rightarrow-\dfrac{5}{6}x=\dfrac{3}{4}+\dfrac{3}{6}-\dfrac{8}{2}-\dfrac{5}{3}\\ \Rightarrow-\dfrac{5}{6}x=\dfrac{9}{12}+\dfrac{6}{12}-\dfrac{48}{12}-\dfrac{20}{12}\\ \Rightarrow-\dfrac{5}{6}x=-\dfrac{53}{12}\\ \Rightarrow x=\left(-\dfrac{53}{12}\right):\left(-\dfrac{5}{6}\right)\\ \Rightarrow x=\dfrac{53}{10}\)

a) Do 97 < 98 nên 97/100 < 98/100 (1)

Do 100 < 99 nên 98/100 > 98/99 (2)

Từ (1) và (2) ⇒ 97/100 < 98/99

b) 19/18 = 1 + 1/18

2021/2020 = 1 + 1/2020

Do 18 < 2020 nên 1/18 > 1/2020

⇒ 1 + 1/18 > 1 + 1/2020

⇒ 19/18 > 2021/2020

c) 13/17 = 130/170 = 1 - 40/170

131/171 = 1 - 40/171

Do 170 < 171 nên 40/170 > 40/171

⇒ 1 - 40/170 < 1 - 40/171

⇒ 13/17 < 131/171

d) Sửa đề: 51/61 và 515/615

51/61 = 510/610 = 1 - 100/610

515/615 = 1 - 100/615

Do 610 < 615 nên 100/610 > 100/615

⇒ 1 - 100/610 < 1 - 100/615

⇒ 51/61 < 515/615

Bài 1:

\(\dfrac{a}{b}-\dfrac{a+2009}{b+2009}=\dfrac{a\left(b+2009\right)-b\left(a+2009\right)}{b\left(b+2009\right)}\)

\(=\dfrac{2009a-2009b}{b\left(b+2009\right)}=\dfrac{2009\left(a-b\right)}{b\left(b+2009\right)}\)

Vì a>b>0 nên a-b>0; b>0; b+2009>0

=>\(\dfrac{2009\left(a-b\right)}{b\left(b+2009\right)}>0\)

=>\(\dfrac{a}{b}>\dfrac{a+2009}{b+2009}\)

a: Xét ΔMAC và ΔMEB có

MA=ME

\(\widehat{AMC}=\widehat{EMB}\)(đối đỉnh)

MC=MB

Do đó: ΔMAC=ΔMEB

=>\(\widehat{MAC}=\widehat{MEB}\)

=>AC//EB

b: Xét ΔIAM và ΔKEM có

MA=ME

\(\widehat{MAI}=\widehat{MEK}\)

AI=EK

Do đó: ΔIAM=ΔKEM

=>\(\widehat{IMA}=\widehat{KME}\)

=>\(\widehat{IMA}+\widehat{AMK}=180^0\)

=>I,M,K thẳng hàng

Đặt 222=a

=>\(\dfrac{222}{222^2+1}=\dfrac{a}{a^2+1};\dfrac{223}{223^2+1}=\dfrac{\left(a+1\right)^2}{\left(a+1\right)^2+1}\)

\(\dfrac{a^2}{a^2+1}-\dfrac{\left(a+1\right)^2}{\left(a+1\right)^2+1}\)

\(=\dfrac{a^2\left[\left(a+1\right)^2+1\right]-\left(a+1\right)^2\left(a^2+1\right)}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)

\(=\dfrac{a^2\left(a^2+2a+2\right)-\left(a^2+2a+1\right)\left(a^2+1\right)}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)

\(=\dfrac{a^4+2a^3+2a^2-a^4-a^2-2a^3-2a-a^2-1}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)

\(=\dfrac{-2a-1}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}< 0\)

=>\(\dfrac{222}{222^2+1}< \dfrac{223}{223^2+1}\)

--5--A Some New World crops were very successful in the Old World.

--3--B Before explorers came to the New World, many familiar foods of today were not available in the New World.

--4--C People from the Old World planted crops in the New World.

--2--D Before explorers came to the New World, many familiar foods of today were not available in the Old World.

--6--E Some New World crops were very expensive in the Old World.

1. Before the fifteenth century, many familiar foods were not available to everyone in the world. True or False? (Par. 2) ----True

2. What kinds of animals did people in the New World raise for food? (Par. 3) ----abcd

a Sheep

b Pigs

c Chickens

d None of these