Cho tam giác ABC hai đường trung tuyến BM và CN cắt nhau tại G.Gọi D và E lần lượt là trung điểm cảu GB và GC. Chứng minh rằng:
a) MN//DE
b) Tứ giác MNDE là hình bình hành
c) ND//ME
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

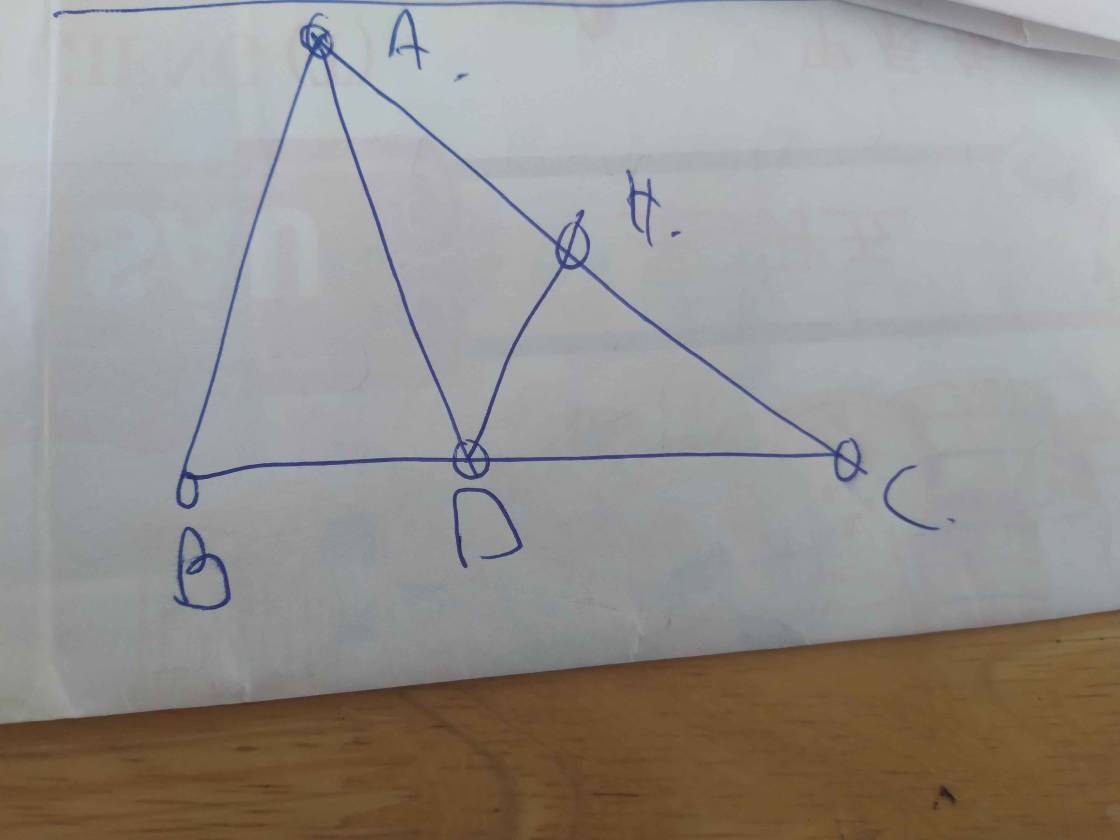
ΔAHC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(AC^2=6^2+8^2=100\)
=>\(AC=\sqrt{100}=10\left(cm\right)\)

Gọi A� là tử (14x2−8x+914�2−8�+9)
C� là mẫu (3x2+6x+93�2+6�+9)
Ta có:A� =14x2−8x+914�2−8�+9
⇒Amin⇒����=557557
Ta có: C�=3x2+6x+93�2+6�+9
⇒Cmin⇒����=6
Suy ra Bmin����=(557)6(557)6=55425542
Vậy GTNN của B là 5542

Nếu ta chạm vào dây điện trần (không có lớp cách điện) dòng điện sẽ truyền qua cơ thể gây co giật, bỏng thậm chí có thể gây chết người là do tác dụng sinh lí của dòng điện

Khi nhúng chìm vật vào nước, vật chịu tác dụng của lực đẩy Ác – si –mét nên chỉ số của lực kế giảm 0,2N, tức là FA = 0,2N.
Ta có: FA = V.dn, trong đó dn là trọng lượng riêng của nước, V là thể tích phần nước bị vật chiếm chỗ.
Vật ngập hoàn toàn trong nước nên Vvật = V.
Thể tích của vật là:
Treo một vật ở ngoài không khí vào lực kế, lực kế chỉ 2,1N nên trọng lượng của vật là: P = 2,1 N.
Suy ra trọng lượng riêng của chất làm vật:
Tỉ số: 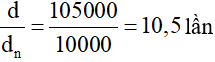


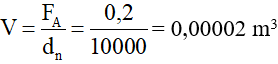
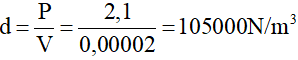
a) Do BM là đường trung tuyến của \(\Delta ABC\left(gt\right)\)
\(\Rightarrow M\) là trung điểm của AC
Do CN là đường trung tuyến của \(\Delta ABC\left(gt\right)\)
\(\Rightarrow N\) là trung điểm của AB
\(\Delta ABC\) có:
M là trung điểm của AC (cmt)
N là trung điểm của AB (cmt)
\(\Rightarrow MN\) là đường trung bình của \(\Delta ABC\)
\(\Rightarrow MN\) // \(BC\) (1)
\(\Delta ABC\) có:
D là trung điểm của GB (gt)
E là trung điểm của GC (gt)
\(\Rightarrow DE\) là đường trung bình của \(\Delta GBC\)
\(\Rightarrow DE\) // \(BC\) (2)
Từ (1) và (2) \(\Rightarrow MN\) // \(DE\)
b) Do MN là đường trung bình của \(\Delta ABC\left(cmt\right)\)
\(\Rightarrow MN=\dfrac{BC}{2}\) (3)
Do DE là đường trung bình của \(\Delta GBC\left(cmt\right)\)
\(\Rightarrow DE=\dfrac{BC}{2}\) (4)
Từ (3) và (4) \(\Rightarrow MN=DE\)
Xét tứ giác MNDE có:
MN // DE (cmt)
\(MN=DE=\dfrac{BC}{2}\left(cmt\right)\)
\(\Rightarrow MNDE\) là hình bình hành
c) Do MNDE là hình bình hành (cmt)
\(\Rightarrow ND=ME\)