Vì 1 chỉ ⋮ 1 nên:

x⁹⁰ =1

x    = 1

Vậy x=1

Giải thích:

Để giải bài toán này, ta sẽ sử dụng các kiến thức về số hạt cơ bản và khối lượng nguyên tử của các nguyên tố.

Lời giải:

a) Gọi số hạt proton, nơtron và electron của nguyên tố X lần lượt là p, n và e.

Theo đề bài, tổng số hạt của nguyên tố X là 40:

p + n + e = 40 (1)

Và số hạt mang điện nhiều hơn số hạt không mang điện là 12:

p + e > n (2)

Từ (1) và (2), ta có thể suy ra số lượng từng loại hạt cơ bản của X.

b) Để xác định tên và kí hiệu tên của nguyên tố X, ta cần biết số hạt proton của nó. Vì số hạt proton chính là số nguyên tử của nguyên tố, nên ta cần tìm giá trị của p.

c) Để tính khối lượng nguyên tử X, ta cần biết khối lượng mỗi hạt cơ bản (proton, nơtron và electron) và số lượng từng loại hạt cơ bản của X.

Lời giải chi tiết cho từng câu hỏi sẽ được cung cấp sau khi có thông tin thêm về số hạt proton của nguyên tố X. 

Ez quá <3

không biết

 Ta thấy \(72=2^3.3^2\) nên a, b có dạng \(\left\{{}\begin{matrix}a=2^x3^y\\b=2^z.3^t\end{matrix}\right.\) với \(x,y,z,t\inℕ\) và \(max\left\{x,z\right\}=3;max\left\{y,t\right\}=2\). 

 Theo đề bài, ta có \(2^x.3^y+2^z.3^t=42\)

 \(\Leftrightarrow2^{x-1}.3^{y-1}+2^{z-1}3^{t-1}=7\)   (*), do đó \(x,y,z,t\ge1\)

 TH1: \(x\ge z,y\le t\). Khi đó \(x=3,t=2\). (*) thành:

 \(4.3^{y-1}+3.2^{z-1}=7\) \(\Leftrightarrow y=z=1\)

 Vậy \(\left\{{}\begin{matrix}a=24\\b=18\end{matrix}\right.\) (nhận)

 TH2: KMTQ thì giả sử \(x\ge z,y\ge t\). Khi đó \(x=3,z=2\). (*) thành 

 \(4.3^{y-1}+2.3^{t-1}=7\), điều này là vô lí.

 Vậy \(\left(a,b\right)=\left(24,18\right)\) hay \(\left(18,24\right)\) là cặp số duy nhất thỏa yêu cầu bài toán.

Ta thấy \(87=1.87=3.29\) nên ta xét 2TH

 TH1: \(\left\{{}\begin{matrix}S\left(n\right)=1\\S\left(n+1\right)=87\end{matrix}\right.\)

 Vì \(S\left(n\right)=1\) nên \(n=100...00\), do đó \(n+1=100...01\) nên \(S\left(n+1\right)=2\), mâu thuẫn.

 TH2: \(\left\{{}\begin{matrix}S\left(n\right)=87\\S\left(n+1\right)=1\end{matrix}\right.\)

 Vì \(S\left(n+1\right)=1\) nên \(n+1=100...00\), do đó \(n=999...99\) chia hết cho 9, dẫn đến \(S\left(n\right)⋮9\), mâu thuẫn với \(S\left(n\right)=87\)

 TH3: \(\left\{{}\begin{matrix}S\left(n\right)=3\\S\left(n+1\right)=29\end{matrix}\right.\)

Vì \(S\left(n\right)=3\) nên \(n⋮3\) \(\Rightarrow n+1\) chia 3 dư 1 \(\Rightarrow S\left(n+1\right)\) chia 3 dư 1. Thế nhưng 29 chia 3 dư 2, vô lý.

 TH4: \(\left\{{}\begin{matrix}S\left(n\right)=29\\S\left(n+1\right)=3\end{matrix}\right.\) . Ta lại xét các TH:

   TH4.1: \(n+1=10...010...01\) hoặc \(200...01\) hoặc \(100...2\). Khi đó trong tất cả các TH thì ta đều có \(S\left(n\right)=2\), không thỏa mãn.

   TH4.2: \(n+1=10...010...010...0\) hoặc \(200...0100...0\) hoặc \(100...020...0\) hoặc \(300...00\). Khi đó trong tất cả các TH thì ta đều có\(S\left(n\right)=2+9m\left(m\inℕ\right)\) với m là số chữ số 9 có trong n. Để chọn được số nhỏ nhất, ta chỉ việc lược bỏ tất cả các số 0 ở giữa và cho \(m=3\) để có \(S\left(n\right)=29\). Vậy, ta tìm được \(n=11999\) (thỏa mãn)

 Vậy, số cần tìm là 11999.

a) Đồ thị:

b) Gọi giao điểm của đồ thị của hàm số y = x - 1 với trục tung, với trục hoành lần lượt là 2 điểm B và C

Thay x = 0 vào hàm số y = x - 1 ta có:

y = 0 - 1 = - 1

⇒ B(0; -1)

Thay y = 0 vào hàm số y = x - 1 ta có:

x - 1 = 0

⇔ x = 1

⇒ C(1; 0)

c) Gọi (t): y = ax + b (a 0)

Do (t) // (d) nên a = -2

⇒ (t): y = -2x + b

Thay y = -3 vào (d') ta có:

x - 1 = -3

⇔ x = -3 + 1

⇔ x = -2

Thay x = -2; y = -3 vào (t) ta có:

-2.(-2) + b = -3

⇔ 4 + b = -3

⇔ b = -3 - 4

⇔ b = -7

Vậy (t): y = -2x - 7

6

6

không biết

19,98 × 147 - 19,98 × 33 - 19,98 × 14

= 19,98 × (147 - 33 - 14)

= 19,98 × 100

= 1998

--------

4,52 : 9 - 1,46 : 9

= (4,52 - 1,46) : 9

= 3,06 : 9

= 0,34

--------

3,65 × 13 + 3,65 × 8 - 3,65

= 3,65 × 13 + 3,65 × 8 - 3,65 × 1

= 3,65 × (13 + 8 - 1)

= 3,65 × 20

= 73

         B = \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{3^3}\) + ... + \(\dfrac{1}{3^{2020}}\) + \(\dfrac{1}{3^{2021}}\) < \(\dfrac{1}{2}\)

       3.B = 1   + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\)+ ... + \(\dfrac{1}{3^{2019}}\) +  \(\dfrac{1}{3^{2020}}\) 

3B - B = 1+\(\dfrac{1}{3}\)+ \(\dfrac{1}{3^2}\) + ... + \(\dfrac{1}{3^{2019}}\) + \(\dfrac{1}{3^{2020}}\) - (\(\dfrac{1}{3}\)+ \(\dfrac{1}{3^2}\)+ ... + \(\dfrac{1}{3^{2020}}\)+\(\dfrac{1}{3^{2021}}\))

 2B    = 1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{3^2}\)+...+ \(\dfrac{1}{3^{2019}}\) + \(\dfrac{1}{3^{2020}}\) - \(\dfrac{1}{3}\) - \(\dfrac{1}{3^2}\)- ...- \(\dfrac{1}{3^{2020}}\)-\(\dfrac{1}{3^{2021}}\)

2B = (1 - \(\dfrac{1}{3^{2021}}\)) + (\(\dfrac{1}{3}\) - \(\dfrac{1}{3}\)) + (\(\dfrac{1}{3^2}\) - \(\dfrac{1}{3^2}\)) +...+ (\(\dfrac{1}{3^{2020}}\) - \(\dfrac{1}{3^{2020}}\))

2B = 1 - \(\dfrac{1}{3^{2021}}\) 

 B  = (1 - \(\dfrac{1}{3^{2021}}\)) : 2

 B = \(\dfrac{1}{2}\) - \(\dfrac{1}{2.3^{2021}}\) < \(\dfrac{1}{2}\) (đpcm)

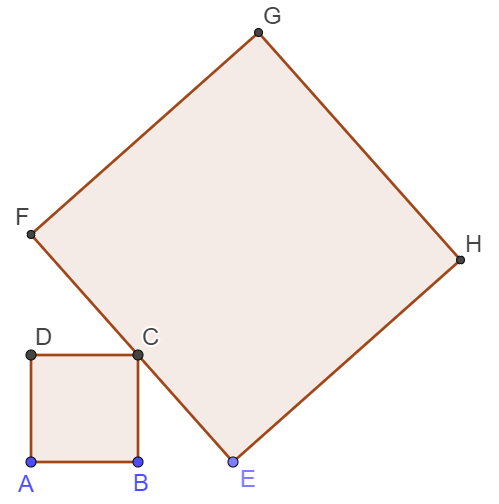
8 góc vuông

2 góc tù

2 góc nhọn 

cạnh AB song song với CD

cạnh EH song song với FG

a) Hình có 8 góc vuông

0 góc tù

2 góc nhọn

b) Cạnh AB song song với cạnh CD

Cạnh EH song song với cạnh FG