\(3+2^{x-1}=24-\left[4^2-\left(2^2-1\right)\right]\)

\(=3+2^{x-1}=24-\left[4^2-\left(4-1\right)\right]\)

\(=3+2^{x-1}=24-\left[16-3\right]\)

\(\Rightarrow3+2^{x-1}=11\)

\(\Rightarrow2^{x-1}=11-3\)

\(\Rightarrow2^{x-1}=8\)

\(\Rightarrow2^{x-1}=2^3\)

\(\Rightarrow x-1=3\)

\(\Rightarrow x=4\)

Vậy \(x=4\)

\(\left(x-6\right)^2=\left(x-6\right)^3\)

\(\Leftrightarrow\left(x-6\right)^2-\left(x-6\right)^3=0\)

\(\Leftrightarrow\left(x-6\right)^2.\left(1-x+6\right)\text{=}0\)

\(\Leftrightarrow\left(x-6\right)^2.\left(7-x\right)\text{=}0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x-6\right)^2\text{=}0\\7-x\text{=}0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\text{=}6\\x\text{=}7\end{matrix}\right.\)

Vậy.......

\(275:25=11:100=\dfrac{11}{100}=0,11\)

275 : 25 = 1100 : 100 = 11

Số ở giữa 2 số là:

\(2550:3=850\)

Vậy số lớn nhất là số liền sau số 850 là số 851

Ba số tự nhiên liên tiếp là : \(n;n+1;n+2\left(n\inℕ\right)\)

Tổng của ba số là :

\(n+n+1+n+2=2550\)

\(\Rightarrow3n+3=2550\)

\(\Rightarrow3\left(n+1\right)=2550\)

\(\Rightarrow n+1=850\)

\(\Rightarrow n=849\)

Số lớn nhất trong 3 số là :

\(n+2=849+2=851\)

Đáp số...

a) \(\left(x^2-7x+12\right).\left(x^2-15x+56\right)-60\)

\(=\left(x-3\right)\left(x-4\right)\left(x-7\right)\left(x-8\right)-60\)

b) \(x^4+2000x^2+1999x+2000\)

\(=\left(x^2-x+2000\right)\left(x^2+x+1\right)\)

\(=\left(x^2+x-1\right)^2+1999\left(x^2+x+1\right)+1\)

hình như Thành lộn đề rồi đấy ạ, ý mình là phân tích thành nhân tử á

Tổng số chiếc điện thoại bán được trong 3 tháng cuối:

\(3\times160=480\) (chiếc)

Tổng số chiếc điện thoại bán được trong cả năm:

\(480+1320=1800\) (chiếc) 

Trung bình mỗi tháng cửa hàng bán được:

\(1800:12=150\) (chiếc)

Đáp số: ...

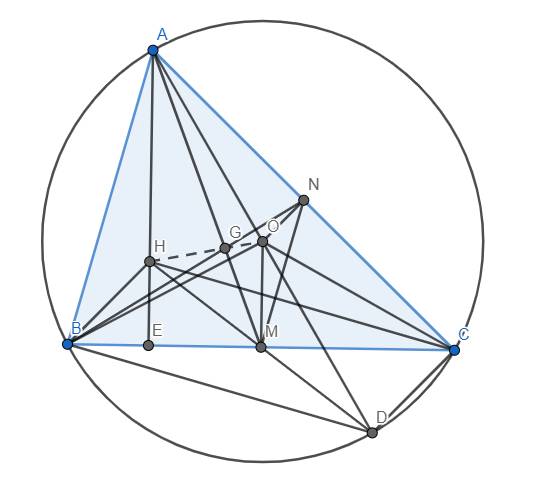
a) Ta chứng minh \(\Delta HAB~\Delta OMN\). Thật vậy, từ đề bài, dễ thấy H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác ABC. Vẽ đường tròn ngoại tiếp này. Dựng đường kính AD của (O). AH cắt BC tại E.

 Ta thấy \(\widehat{ACD}=\widehat{AEB}\left(=90^o\right)\) và \(\widehat{ADC}=\widehat{ABE}\) (góc nội tiếp cùng chắn \(\stackrel\frown{AC}\)). \(\Rightarrow\Delta ACD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\widehat{BAH}=\widehat{CAO}\)

 Mà \(\widehat{CAO}=\widehat{OCA}\), thêm vào đó tứ giác OMCN nội tiếp (vì \(\widehat{OMC}=\widehat{ONC}=90^o\)) nên \(\widehat{OMN}=\widehat{OCN}\). Do đó \(\widehat{HAB}=\widehat{OMN}\)

 Hoàn toàn tương tự, ta suy ra \(\widehat{HBA}=\widehat{ONM}\). Từ đó suy ra \(\Delta HAB~\Delta OMN\left(g.g\right)\) (đpcm)

b) Ta thấy BH//CD\(\left(\perp AC\right)\) và CH//BD\(\left(\perp AB\right)\) nên tứ giác BDCH là hình bình hành. Mà M là trung điểm BC nên M cũng là trung điểm của DH. Lại có O là trung điểm của AD nên OM là đường trung bình của tam giác DHA \(\Rightarrow\left\{{}\begin{matrix}OM//AH\\OM=\dfrac{1}{2}AH\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\widehat{HAG}=\widehat{GMO}\\\dfrac{AH}{OM}=\dfrac{GA}{GM}\left(=2\right)\end{matrix}\right.\)

\(\Rightarrow\Delta AHG~\Delta MOG\left(c.g.c\right)\) (đpcm)

c) Từ \(\Delta AHG~\Delta MOG\Rightarrow\widehat{AGH}=\widehat{MGO}\)

Do A, G, M thẳng hàng nên \(\widehat{AGH}+\widehat{HGM}=180^o\) 

Từ đó suy ra \(\widehat{HGM}+\widehat{MGO}=180^o\) \(\Rightarrow\) H, O, G thẳng hàng.

Số đó cộng với 10 bằng:

\(50+20=70\)

Số cần tìm là:

\(70-10=60\)

Đáp số: 60 

so can tim la

    50 + 20 - 10 = 60

Ta có : a . b = ƯCLN ( a ; b ) . BCNN ( a ; b ) 

Mà a . b = 2940 và BCNN ( a ; b ) = 210

⇒⇒ ƯCLN ( a ; b ) = 2940 : 210 = 14

⇒⇒ a = 14m ; b = 14n ( m ; n > 0 ) 

Thay a = 14m ; b = 14n vào a . b = 2940, ta được :

        14m . 14n = 2940

        196 . m . n = 2940

                m . n  = 15

⇒⇒ m ; n ∈ Ư ( 15 ) = { 1 ; 3 ; 5 ; 15 }

+, Với m = 1 ; n = 15 ⇒⇒ a = 14 ; b = 210

+, Với m = 3 ; n = 5 ⇒⇒ a = 42 ; b = 70

+, Với m = 5 ; n = 3 ⇒⇒ a = 70 ; b = 42

+, Với m = 15 ; n = 1 ⇒⇒ a = 210 ; b = 14 

 Vậy ( a ; b ) ∈ { ( 14 ; 210 ) ; ( 42 ; 70 ) ; ( 70 ; 42 ) ; ( 210 ; 14 ) } 

ab = UCLN ( a,b); BCNN ( a,b )

=> UCLN (a,b) = 2940 : 210 = 14

Vậy a = 14m và b = 14n ( m > hoặc = n )

Thay a.b = 2940 ta có: 

14m . 14n = 2940 

=> m.n = 2940 : ( 14 x 14 ) = 15 

Vì m > hoặc = n nên 15 = 5.3 = 15.1

Với m = 5; n = 3 => a = 70 ; b = 42

Với m = 15; n = 1 => a = 210; b = 1

Vì \(BCNN\left(a,b\right)=300\) và \(ƯCLN\left(a,b\right)=15\)

\(\Leftrightarrow a.b=300.15=4500\)

Vì \(ƯCLN\left(a,b\right)=15\) nên \(a=15m\) và \(b=15n\) với \(ƯCLN=\left(m,n\right)=1\)

Vì \(a+15=b\Rightarrow15m+15=15n\Rightarrow15\left(m+1\right)=15n\)

\(\Leftrightarrow m+1=n\)

Mà \(a.b=4500\Rightarrow15m.15n=4500\Rightarrow15.15.m.n=4500\)

\(\Leftrightarrow m.n=20\)

\(\Leftrightarrow m=1\) và \(n=20\) hoặc \(m=4\) và \(n=5\)

Lời giải:
Đặt $A=1-2+2^2-2^3+2^4-2^5+2^6-....-2^{2021}+2^{2022}$

$A=1+(-2+2^2-2^3)+(2^4-2^5+2^6)+(-2^7+2^8-2^9)+...+(2^{2020}-2^{2021}+2^{2022})$

$A=1+(-2+2^2-2^3)+2^3(2-2^2+2^3)+2^6(-2+2^2-2^3)+....+2^{2019}(2-2^2+2^3)$

$=1+(-6)+2^3.6+2^6(-6)+....+2^{2019}.6$

$=1+6(-1+2^3-2^6+...+2^{2019})$

Suy ra $A$ chia $6$ dư $1$/