cho a,b,c dương va a+b+c=3 . Tìm Pmax = a/a+\(\sqrt{3a+bc}\) + b/b+\(\sqrt{3b+ca}\)+c/c+\(\sqrt{3c+ab}\) ai giúp mình bài bđt này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Với m = 1, ta có:
⇒ (d): y = x - 1/2 + 2 = x + 3/2
Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = x + 3/2
⇔ x² = 2x + 3
⇔ x² - 2x - 3 = 0
Do a - b + c = 1 - (-2) + 3 = 0 nên phương trình có hai nghiệm:
x₁ = -1; x₂ = -c/a = 3
x₁ = -1 ⇒ y = 1/2 . (-1)² = 1/2
⇒ A(-1; 1/2)
x₂ = 3 ⇒ y = 1/2 . 3² = 9/2
⇒ B(3; 9/2)
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = mx - 1/2 m² + m + 1
⇔ x² = 2mx - m² + 2m + 2
⇔ x² - 2mx + m² - 2m - 2
∆' = (-m)² - 1.(m² - 2m - 2)
= m² - m² + 2m + 2
= 2m + 2
Để phương trình có hai nghiệm phân biệt thì ∆' > 0
⇔ 2m + 2 > 0
⇔ 2m > -2
⇔ m > -1
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = 2m
x₁x₂ = m² - 2m - 2
Ta có:
|x₁ - x₂| = (x₁ - x₂)² = [(x₁ + x₂)² - 4x₁x₂]
= [(2m)² - 4.(m² - 2m - 2)]
= (4m² - 4m² + 8m + 4)
= 8m + 4
= 2(2m + 2)
Mà |x₁ - x₂| = 2
⇔ 2(2m + 2) = 2
⇔ (2m + 2) = 1
⇔ 2m + 2 = 1
⇔ 2m = -1
⇔ m = -1/2 (nhận)
Vậy m = -1/2 thì phương trình có hai nghiệm phân biệt thỏa mãn |x₁ - x₂| = 2


\(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot\left(m-3\right)\)
=1-4(m-3)
=1-4m+12
=-4m+13
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>-4m+13>0
=>-4m>-13
=>\(m< \dfrac{13}{4}\)

a: Phương trình hoành độ giao điểm là:
\(x^2=-x+6\)
=>\(x^2+x-6=0\)
=>(x+3)(x-2)=0
=>\(\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
Thay x=2 vào y=-x+6, ta được:
y=-2+6=4
Thay x=-3 vào y=-x+6, ta được:
y=-(-3)+6=9
Vậy: Tọa độ giao điểm là A(2;4); B(-3;9)
b: O(0;0); A(2;4); B(-3;9)
\(OA=\sqrt{\left(2-0\right)^2+\left(4-0\right)^2}=2\sqrt{5}\)
\(OB=\sqrt{\left(-3-0\right)^2+\left(9-0\right)^2}=3\sqrt{10}\)
\(AB=\sqrt{\left(-3-2\right)^2+\left(9-4\right)^2}=5\sqrt{2}\)
Xét ΔOAB có \(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{20+90-50}{2\cdot2\sqrt{5}\cdot3\sqrt{10}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinAOB=\dfrac{1}{\sqrt{2}}\)
Diện tích tam giác AOB là:
\(S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB\cdot sinAOB\)
\(=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{2}}\cdot2\sqrt{5}\cdot3\sqrt{10}=15\)
Lời giải:
a. PT hoành độ giao điểm của $(d)$ và $(P)$:
$x^2=-x+6$
$\Leftrightarrow x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
Với $x=2$ thì $y=x^2=4$. Ta có giao điểm thứ nhất $(2;4)$
Với $x=-3$ thì $y=x^2=9$. Ta có giao điểm thứ hai $(-3;9)$
b.
Đặt $A(2,4)$ và $B(-3;9)$
$AB=\sqrt{(2--3)^2+(4-9)^2}=5\sqrt{2}$
Gọi $C,D$ là giao điểm của $(d)$ và $Ox, Oy$
$C\in Ox$ nên $y_C=0$
$C\in (d)$ nên: $x_C=6-y_C=6-0=6$. Vậy $C$ có tọa độ $(6;0)$
$D\in Oy$ nên $x_D=0$
$D\in (d)$ nên: $y_D=-x_D+6=-0+6=6$. Vậy $D$ có tọa độ $(0;6)$
$CD=\sqrt{(6-0)^2+(0-6)^2}=6\sqrt{2}$
$S_{OCD}=\frac{OC.OD}{2}=\frac{|x_C|.|y_D|}{2}=\frac{6.6}{2}=18$
$\frac{S_{OAB}}{S_{OCD}}=\frac{AB}{CD}=\frac{5\sqrt{2}}{6\sqrt{2}}=\frac{5}{6}$
$\Rightarrow S_{OAB}=\frac{5}{6}S_{OCD}=\frac{5}{6}.18=15$

Lời giải:
a.
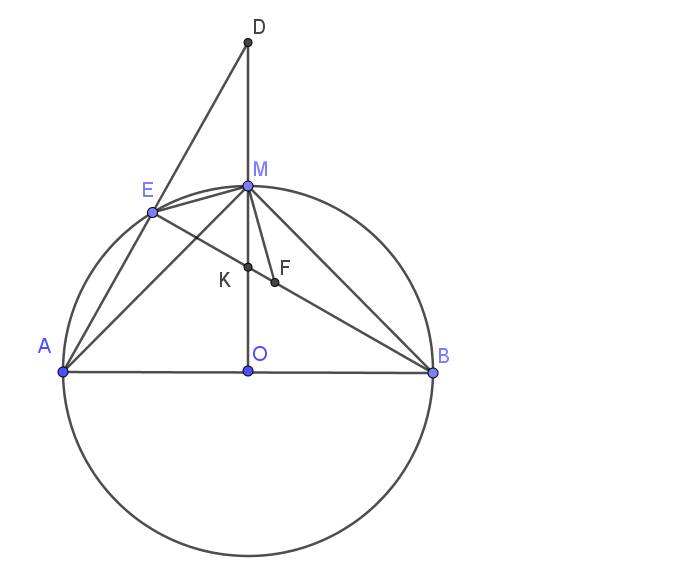
Vì $M$ là điểm chính giữa cung $AB$ nên $OM\perp AB$
$\Rightarrow \widehat{KOA}=\widehat{MOA}=90^0$
Lại có: $\widehat{AEK}=\widehat{AEB}=90^0$ (góc nt chắn nửa đường tròn)
Xét tứ giác $EAOK$ có tổng hai góc đối nhau $\widehat{KOA}+\widehat{AEK}=90^0+90^0=180^0$
$\Rightarrow EAOK$ là tgnt.
b.
Xét tam giác $EAM$ và $FBM$ có:
$AM=BM$ (do $M$ nằm chính giữa cung AB)
$EA=FB$
$\widehat{EAM}=\widehat{EBM}=\widehat{FBM}$ (góc nt chắn cung $EM$)
$\Rightarrow \triangle EAM=\triangle FBM$ (c.g.c)
$\Rightarrow EM=FM(1)$
Và $\widehat{EMA}=\widehat{FMB}$
$\Rightarrow \widehat{EMA}+\widehat{MAF}=\widehat{FMB}+\widehat{MAF}=\widehat{AMB}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow \widehat{EMF}=90^0(2)$
Từ $(1); (2)$ suy ra $EMF$ là tam giác vuông cân tại $M$
c.
Vì $EMF$ vuông cân tại $M$ nên $\widehat{MEK}=45^0$
$\widehat{DEM}=180^0-\widehat{AEB}-\widehat{MEK}=180^0-90^0-45^0=45^0$
$\Rightarrow \widehat{DEM}=\widehat{MEK}$
$\Rightarrow EM$ là phân giác trong của $\widehat{DEK}$
$\Rightarrow \frac{MK}{MD}=\frac{EK}{ED}$
$\Rightarrow MK.ED=EK.MD$ (đpcm)

1:
Để (d) cắt (d1) thì \(-\left(k-3\right)\ne2\)
=>\(k-3\ne-2\)
=>\(k\ne1\)
Thay x=-1 vào (d1), ta được:
\(y=2\cdot\left(-1\right)=-2\)
Thay x=-1 và y=-2 vào (d), ta được:
\(-\left(k-3\right)\cdot\left(-1\right)+k-2=-2\)
=>\(k-3+k-2=-2\)
=>2k-5=-2
=>2k=3
=>k=1,5(nhận)
2:
a: Phương trình hoành độ giao điểm là:
\(x^2=-\left(k-3\right)x+k-2\)
=>\(x^2+\left(k-3\right)x-k+2=0\)
\(\text{Δ}=\left(k-3\right)^2-4\cdot1\left(-k+2\right)\)
\(=k^2-6k+9+4k-8=k^2-2k+1=\left(k-1\right)^2\)>=0 với mọi k
=>(P) luôn cắt (d)
b:
ĐKXĐ: k<=2
Theo vi-et, ta có:
\(x_1+x_2=-\dfrac{b}{a}=-k+3;x_1x_2=\dfrac{c}{a}=-k+2\)
\(\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=x_1+x_2+2\sqrt{x_1x_2}\)
\(=-k+3+2\sqrt{-k+2}\)
\(=\left(-k+2\right)+2\sqrt{-k+2}+1=\left(\sqrt{-k+2}+1\right)^2\)
=>\(\sqrt{x_1}+\sqrt{x_2}=\sqrt{-k+2}+1\)
\(\sqrt{x_1}+\sqrt{x_2}-x_1x_2=k\)
=>\(\sqrt{-k+2}+1-\left(-k+2\right)=k\)
=>\(\sqrt{-k+2}+1+k-2-k=0\)
=>\(\sqrt{-k+2}-1=0\)
=>-k+2=1
=>-k=-1
=>k=1(nhận)

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
\(P\geq \frac{(a^2+b^2+c^2)^2}{b+2c+c+2a+a+2b}=\frac{(a^2+b^2+c^2)^2}{3(a+b+c)}=\frac{(a^2+b^2+c^2)^2}{9}\)
Tiếp tục áp dụng BĐT Cauchy Schwarz:
$a^2+b^2+c^2\geq \frac{(a+b+c)^2}{1+1+1}=\frac{(a+b+c)^2}{3}=\frac{3^2}{3}=3$
$\Rightarrow P\geq \frac{3^2}{9}=1$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c=1$
Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.

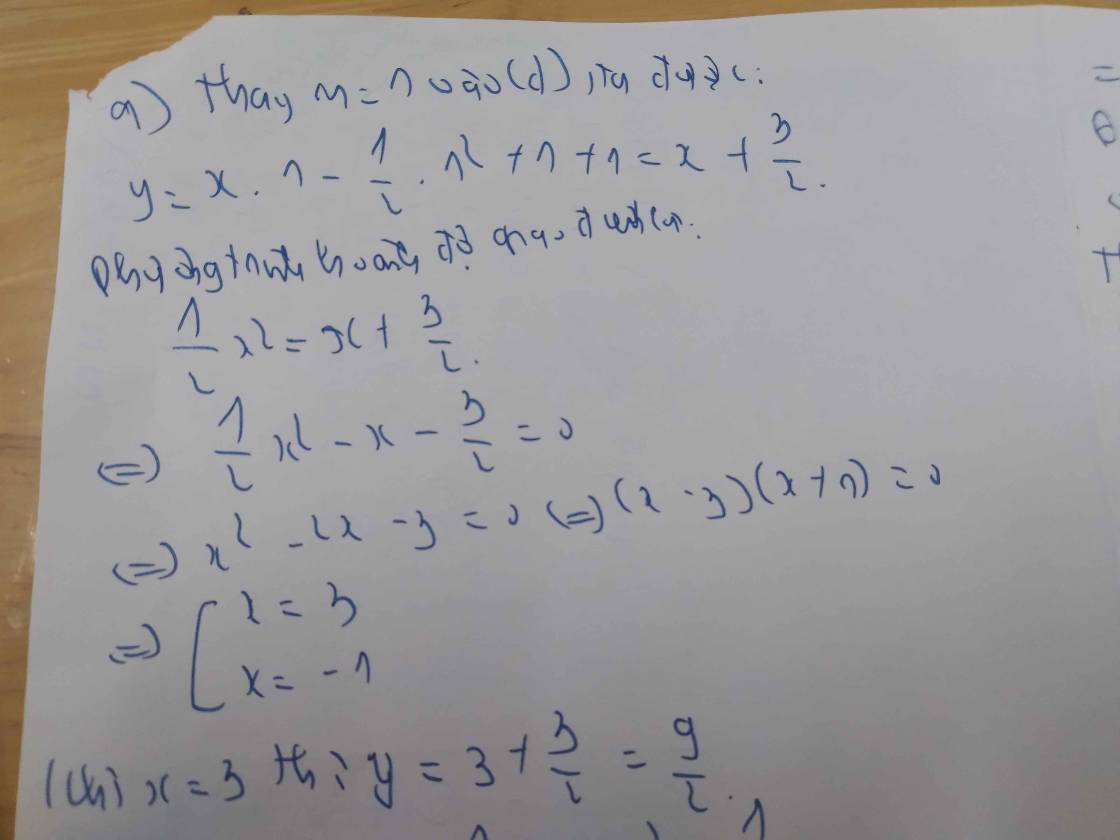


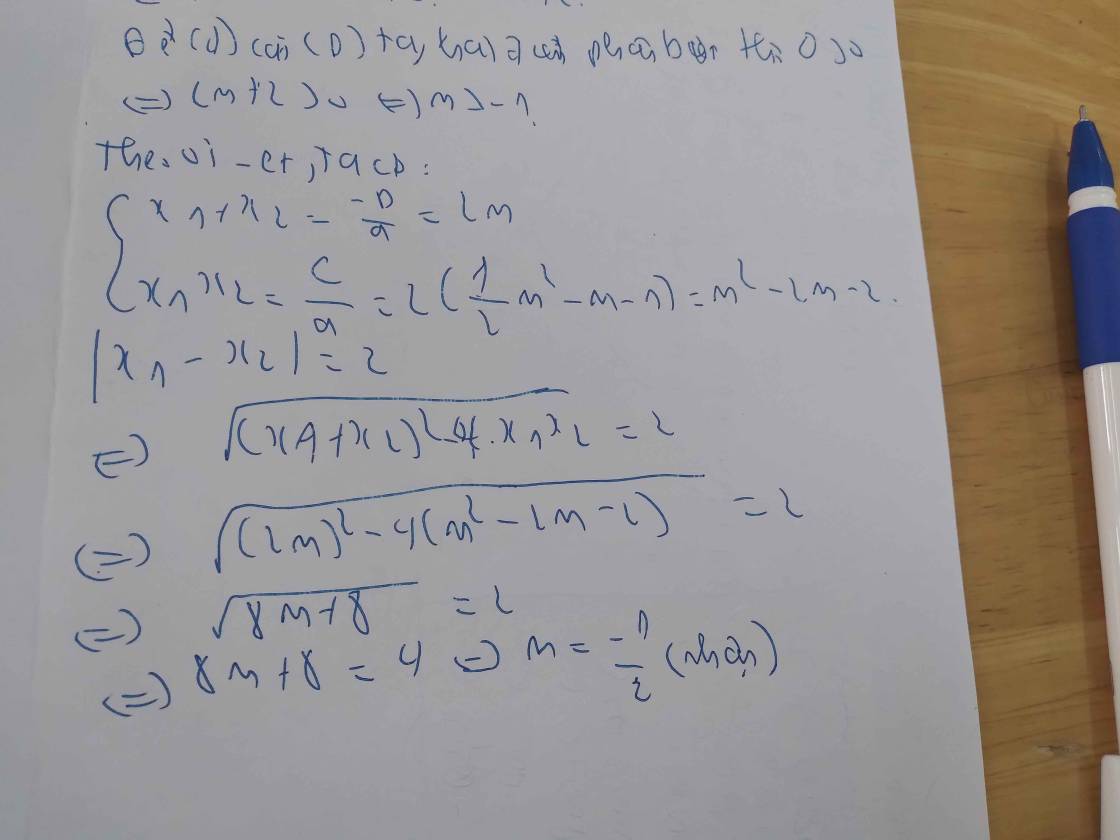

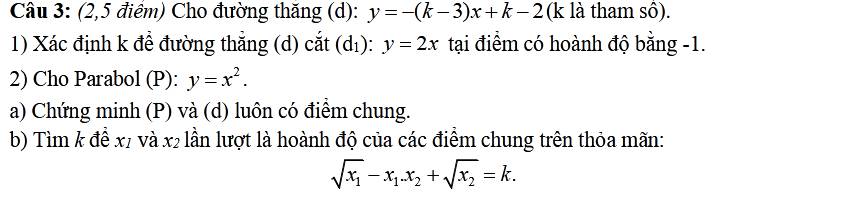

Để tìm giá trị lớn nhất của biểu thức \( P \), ta sẽ sử dụng bất đẳng thức Cauchy-Schwarz (hay bất đẳng thức Buniakovskii):
Đặt \( x = \sqrt{a}, y = \sqrt{b}, z = \sqrt{c} \), ta có \( a = x^2, b = y^2, c = z^2 \).
Biểu thức \( P \) sẽ trở thành:
\[ P = \frac{x^2}{x^2+3} + \frac{y^2}{y^2+3} + \frac{z^2}{z^2+3} + \frac{xy}{3x+z} + \frac{yz}{3y+x} + \frac{zx}{3z+y} \]
Sử dụng bất đẳng thức Cauchy-Schwarz, ta có:
\[ P \geq \frac{(x+y+z)^2}{x^2+y^2+z^2+3(x+y+z)} + \frac{(xy+yz+zx)^2}{3(xy+yz+zx)+xy(x+y+z)} \]
Do \( x+y+z = \sqrt{a} + \sqrt{b} + \sqrt{c} \leq \sqrt{3(a+b+c)} = 3 \), và \( xy+yz+zx \leq \frac{(x+y+z)^2}{3} \), ta có:
\[ P \geq \frac{9}{9+9} + \frac{\frac{(x+y+z)^2}{9}}{3 \times \frac{(x+y+z)^2}{9} + \frac{(x+y+z)^3}{27}} \]
\[ = \frac{1}{2} + \frac{1}{3+\frac{1}{3}} \]
\[ = \frac{1}{2} + \frac{1}{\frac{10}{3}} \]
\[ = \frac{1}{2} + \frac{3}{10} \]
\[ = \frac{8}{10} = \frac{4}{5} \]
Vậy, giá trị lớn nhất của \( P \) là \( \frac{4}{5} \), đạt được khi \( a = b = c = 1 \).