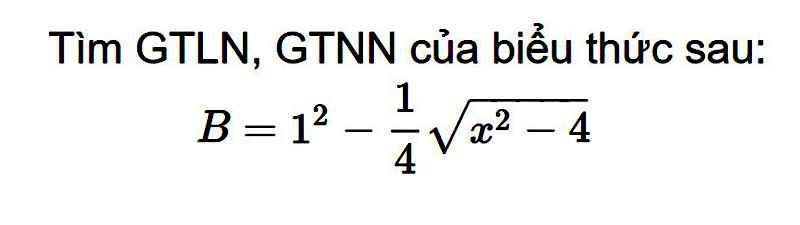
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


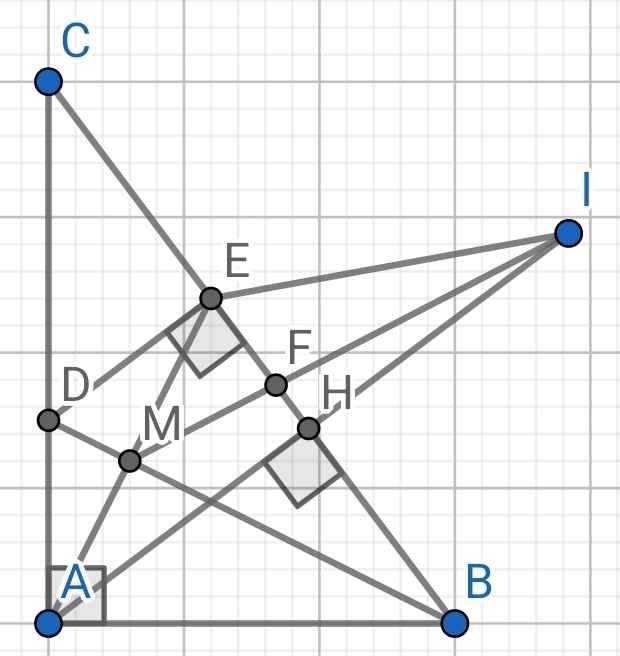
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét hai tam giác vuông: ∆ABD và ∆EBD có:
BD chung
∠ABD = ∠EBD (cmt)
⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)
b) Do HA = HI (gt)
⇒ H là trung điểm của AI
Mà AH ⊥ BC tại H (gt)
⇒ AI ⊥ BC
⇒ BC là đường trung trực của AI
Mà E ∈ BC
⇒ EA = EI
c) Do ∆ABD = ∆EBD (cmt)
⇒ BA = BE (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AE (1)
Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AE
Mà M là giao điểm của BD và AE
⇒ M là trung điểm của AE
⇒ IM là đường trung tuyến của ∆AIE
Lại có:
H là trung điểm của AE (cmt)
⇒ EH là đường trung tuyến của ∆AIE
∆AIE có:
IM là đường trung tuyến (cmt)
EH là đường trung tuyến (cmt)
Mà IM cắt EH tại F
⇒ F là trọng tâm của ∆AIE
d) Do F là trọng tâm của ∆AIE (cmt)
⇒ HF < HE
⇒ AF < AE (quan hệ giữa đường xiên và hình chiếu)
Lại có:
F nằm trên đường trung trực của AI (do BC là đường trung trực của AI)
⇒ AF = IF
Do F là trọng tâm của ∆AIE (cmt)
⇒ IF = 2MF
Do M là trung điểm của AE (cmt)
⇒ AE = 2ME
Mà AF < AE (cmt)
⇒ AF < 2ME
Mà AF = IF (cmt)
⇒ IF < 2ME
Mà IF = 2MF (cmt)
⇒ 2MF < 2ME
⇒ MF < ME
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔEHA vuông tại H và ΔEHI vuông tại H có
EH chung
HA=HI
Do đó: ΔEHA=ΔEHI
=>EA=EI
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại M và M là trung điểm của AE
Xét ΔAEI có
EH,IM là các đường trung tuyến
EH cắt IM tại F
Do đó: F là trọng tâm của ΔAEI

Schools typically have breaks during Tet holiday and the summer.
Schools typically have breaks during the summer and Tet holiday

\(B=\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+...+\dfrac{1}{44\cdot49}\)
\(=\dfrac{1}{5}\left(\dfrac{5}{4\cdot9}+\dfrac{5}{9\cdot14}+...+\dfrac{5}{44\cdot49}\right)\)
\(=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+...+\dfrac{1}{44}-\dfrac{1}{49}\right)\)
\(=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{49}\right)=\dfrac{1}{5}\cdot\dfrac{45}{196}=\dfrac{9}{196}\)


a: ĐKXĐ: x<>1
Để E là số nguyên thì \(3-x⋮x-1\)
=>\(x-3⋮x-1\)
=>\(x-1-2⋮x-1\)
=>\(-2⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{2;0;3;-1\right\}\)
b: \(E=\dfrac{3-x}{x-1}=\dfrac{-\left(x-3\right)}{x-1}=\dfrac{-\left(x-1-2\right)}{x-1}=-1+\dfrac{2}{x-1}\)
Để E min thì x-1=-1
=>x=0

ĐKXĐ: \(x>=\dfrac{5}{6}\)
\(4\sqrt{\dfrac{x}{5}-\dfrac{1}{6}}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(-4\sqrt{\dfrac{x}{5}-\dfrac{1}{6}}< =0\forall x\) thỏa mãn ĐKXĐ
=>\(B=-4\sqrt{\dfrac{x}{5}-\dfrac{1}{6}}+\dfrac{1}{12}< =\dfrac{1}{12}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\dfrac{x}{5}-\dfrac{1}{6}=0\)
=>\(\dfrac{x}{5}=\dfrac{1}{6}\)
=>\(x=\dfrac{5}{6}\)

Em phải viết số theo đúng với đề bài thì mới biết vị trí của que diêm để di chuyển chứ em?
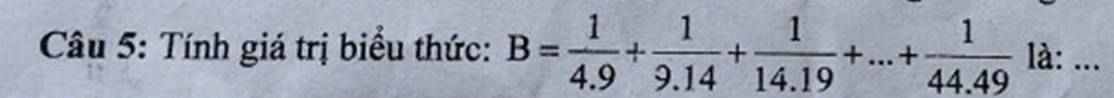

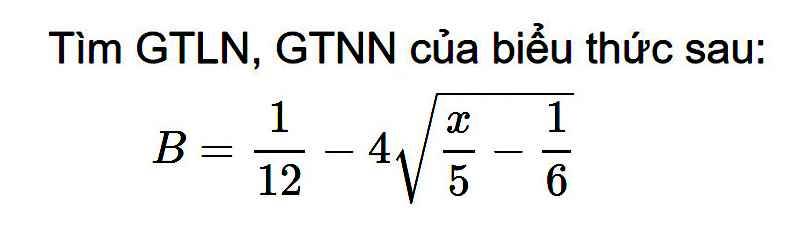
ĐKXĐ: \(\left[{}\begin{matrix}x>=2\\x< =-2\end{matrix}\right.\)
\(\dfrac{1}{4}\sqrt{x^2-4}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{1}{4}\sqrt{x^2-4}< =0\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{1}{4}\sqrt{x^2-4}+1< =1\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(x^2-4=0\)
=>\(x^2=4\)
=>\(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)