1) 

g) \(24+5x\text{=}7^5:7^3\)

\(24+5x\text{=}7^{5-3}\)

\(24+5x\text{=}7^2\text{=}49\)

\(5x\text{=}49-24\text{=}25\)

\(x\text{=}5\)

h) \(x:2^2\text{=}2^3\)

\(x\text{=}2^3.2^2\)

\(x\text{=}2^5\text{=}32\)

2) 

a) \(2^{10}.8.2^3\text{=}2^{10}.2^3.2^3\text{=}2^{10+3+3}\text{=}2^{16}\)

\(b)3^5:27\text{=}3^5:3^3\text{=}3^{5-3}\text{=}3^2\)

\(c)5^2.125\text{=}5^2.5^3\text{=}5^{2+3}\text{=}5^5\)

\(d)6^6:36\text{=}6^6:6^2\text{=}6^{6-2}\text{=}6^4\)

1.

g) \(24+5x=7^5:7^3\left(=7^{5-3}\right)\) -> Trong ngoặc ko cần viết nha

\(24+5x=7^2=49\)

\(5x=49-24\)

\(5x=25\)

\(x=25:5\)

\(=>x=5\)

h) \(x:2^2=2^3\)

\(x=2^3.2^2\)

\(=>x=2^5\)

2.

a) \(2^{10}.8.2^3=2^{10}.\left(2^3\right)2^3=2^{10+3+3}=2^{16}\)

b) \(3^5:27=3^5:\left(3^3\right)=3^{5-3}=3^2\)

c) \(5^2.125=5^2.\left(5^3\right)=5^{2+3}=5^5\)

d) \(6^6:36=6^6:\left(6^2\right)=6^{6-2}=6^4\)

Công thức:

\(a^m.a^n=a^{m+n}\)

\(a^m:a^n=a^{m-n}\)

\(#Wendy.Dang\)

A)23/42-10/21

B)16/25-3/15

C)7/8-1/3-1/2

D)15/7-4/9-10/9

Vì \(b^2=ac\) ta suy ra \(\dfrac{a}{b}=\dfrac{b}{c}\). Đặt \(a=kb\) và \(b=kc\).

Khi đó \(\dfrac{a}{c}=\dfrac{k\left(kc\right)}{c}=k^2\). (1)

Từ tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{2012b}{2012c}=\dfrac{a+2012b}{b+2012c}=k\), suy ra \(k^2=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\). (2)

Từ (1) và (2) suy ra \(k^2=\dfrac{a}{c}=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\) (đpcm)

1.

a) \(2^x=128\)

\(2^x=2^7\)

\(=>x=7\)

b) \(8^{x-1}=64\)

\(8^{x-1}=8^2\)

\(=>x-1=2\)

\(x=2+1\)

\(=>x=3\)

c) \(3+3^x=30\)

\(3^x=30-3\)

\(3^x=27=3^3\)

\(=>x=3\)

d) \(\left(x+2\right)=64\) -> đề có thiếu không vậy?

e) \(3^2.x=3^5\)

\(x=3^5:3^2\)

\(=>x=3^3=27\)

f) \(\left(2x-1\right)^3=343\)

\(\left(2x-1\right)^3=7^3\)

\(=>2x-1=7\)

\(2x=7+1\)

\(2x=8\)

\(x=8:2\)

\(=>x=4\)

\(#Wendy.Dang\) 

a,\(2^x\)=128           b,\(8^{x-1}\)=64              c,3+\(3^x\)=30           d,x+2=64

\(2^7\)=128               \(8^{x-1}\)=\(8^2\)                 \(3^x\)=30-3                  x=64-2

=>x=7              =>x-1=2                  \(3^x\)=27                      x=62

                         x=2+1=3                \(3^x\)=\(3^3\)

                                                     =>x=3

e,\(3^2\).x=\(3^5\)                             f,(2x-\(1^3\))=343

x=\(3^5\):\(3^2\)                                 2x=1+343

x=27                                     2x=344

                                               x=344:2

                                               x=172

10

x - 5 = 25 : 5 

x - 5 = 5 

        x = 5 + 5 

        x = 10 

đáp án đây bn nhé 

chúc bn hok tốt 

Tổng độ dài đáy lớn và đáy bé của hình thang ABCD là: 

     29,43 x 2: 3,6 =  16,35 (m²)

Gọi độ dài đáy lớn là: \(x\) (m); \(x\) > 0

Thì độ dài đáy bé là: \(x\) - 7,5 (m)

Theo bài ra ta có phương trình:  \(x\) + \(x\) - 7,5 = 16,35 

                                                    2\(x\)              = 16,35 + 7,5

                                                    2\(x\)               = 23,85

                                                       \(x\)               = 23,85:2

                                                       \(x\)               = 11,925 (m)

Dộ dài đáy bé của hình thang ABCD là: 11,925 - 7,5 = 4,425 (m)

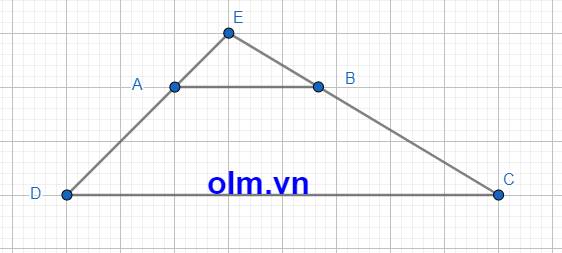
AE = DE - AD = \(\dfrac{3}{2}\)AD - AD = \(\dfrac{1}{2}\)AD
 

⇒S_AEB = \(\dfrac{1}{2}\)S_{ABD (Vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy DE và AE = \(\dfrac{1}{2}\)AD)}

S_ABD = 4,425 x 3,6 : 2 = 7,965 (m²)

S_ABE = 7,965 : 2 = 3,9825 (m²)

\(2\left(x-7\right)=24\)

\(x-7=24:2\)

\(x-7=12\)

\(x=12+7\)

\(\Rightarrow x=19\)

x-7=24:2

x-7 =12

x=12+7 

x=19

Ta đặt:  \(S_{BEMF}=S_1;S_{ABC}=S\)

Kẻ \(AK\perp BC\) ; \(AK\) cắt \(EM\left\{H\right\}\)

Ta có: \(S_1=EM.HK\)

\(\Leftrightarrow S=\dfrac{1}{2}BC.AK\)

\(\Leftrightarrow\dfrac{S_1}{S}=2\dfrac{EM}{BC}.\dfrac{KH}{AK}\)

Đặt \(MA=x;MC=y\) . Theo định lý Thales ta có:

\(\dfrac{EM}{BC}=\dfrac{x}{x+y};\dfrac{HK}{AK}=\dfrac{x}{x+y}\)

\(\Leftrightarrow\dfrac{S_1}{S}=\dfrac{2xy}{\left(x+y\right)^2}\)

Áp dụng bất đẳng thức Cosi dạng \(\dfrac{ab}{\left(a+b\right)^2}\le\dfrac{1}{4}\) ta được:

\(\dfrac{S_1}{S}=\dfrac{2xy}{\left(x+y\right)^2}\le\dfrac{1}{2}\) hay \(S_1\le\dfrac{1}{2}S\)

\(\Leftrightarrow MaxS_1=\dfrac{1}{2}S\)

\(\Leftrightarrow\) \(M\) là trung điểm của \(AC\)

Bạn xem lại đề bài.

Bạn xem lại đề

a) Ta có : t/g ABCD là hbh 

Suy ra : AB//CD

Suy ra : góc FAE = góc AED ( 2 góc ở vị trí slt)

Mà  góc FAE = góc DAE ( AE là tia p/g của góc A )

Suy ra : góc DAE = góc DEA 

Suy ra : tam giác ADE cân tại D

b) CMTT : tam giác FBC cân tại B ( như phần a )

Suy ra : BC = BF 

c) Từ (a) suy ra : AD=DE ( tam giác ADE cân tại D )

 Mà BC=BF ( theo b )

Suy ra : BF=BC=AD=DE 

Suy ra : DE=BF

d) Từ c) suy ra : DE=BF

Ta có : AB = AF+FB

           CD=DE+CE

Mà : DE=BF ; AB=CD ( ABCD là hbh )

Suy ra : AF=CE

Xét t/g AECF có : AF//CE ( AB//CD)

                           AF=CE ( cmt )

Suy ra : t/g AECF là hbh.