Lời giải:
Để $10x^3-2x^4\vdots \frac{3}{7}x^n$ thì $n\leq 3$

Mà $n$ là số tự nhiên nên $\Rightarrow n\in \left\{0; 1; 2;3\right\}$

Vậy có 4 giá trị $n$ thỏa mãn.

Lời giải:
$4n^3-4n^2-n+4=2n^2(2n-1)-n(2n-1)-(2n-1)+3$

$=(2n-1)(2n^2-n-1)+3$

Do đó để $4n^3-4n^2-n+4\vdots 2n-1$ thì:

$3\vdots 2n-1$
$\Rightarrow 2n-1\in\left\{1; -1;3;-3\right\}$

$\Rightarrow n\in \left\{1; 0; 2; -1\right\}$

Mà $n$ là số nguyên dương nên $n\in \left\{1;2\right\}$

`#3107.101107`

`5x^2y(3x^3 - 4y + 5xy) - 15x^5y + 20x^2y^2`

`= 15x^5y - 20x^2y^2 + 25x^3y^2 - 15x^5y + 20x^2y^2`

`= (15x^5y - 15x^5y) + (-20x^2y^2 + 20x^2y^2) + 25x^3y^2`

`= 25x^3y^2`

_______

`(8x^5y^2 + 4x^3y^3 - 2x^6y^2) \div 2x^3y`

`= 4x^2y + 2y^2 - x^3y`

A = ax⁴ - 6 + x³ + x² - 13x + bx³

= ax⁴ + (1 + b)x³ + x² - 13x - 6

Do A là đa thức bậc 2

⇒ a = 0 và 1 + b = 0

*) 1 + b = 0

b = -1

⇒ (3a + b)² = (3.0 - 1)² = (-1)² = 1

a) \(\left(-3x^5y\right)\cdot\left(-2x^2y^2\right)\)

\(=\left[\left(-3\right)\cdot\left(-2\right)\right]\left(x^5\cdot x^2\right)\left(y\cdot y^2\right)\)

\(=6x^7y^3\)

b) \(\left(2x+3y^2\right)\) đã được rút gọn rồi nhé!

Lời giải:
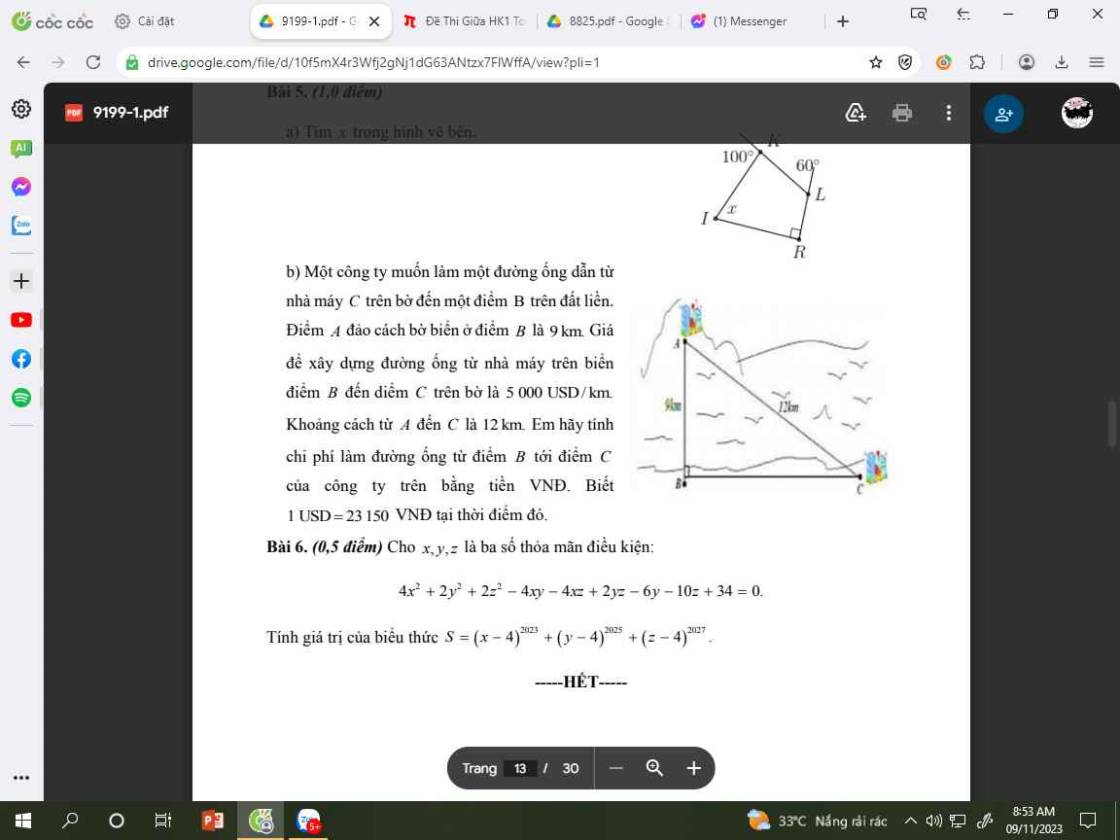
$4x^2+2y^2+2z^2-4xy-4xz+2yz-6y-10z+34=0$

$(4x^2+y^2+z^2-4xy-4xz+2yz)+y^2+z^2-6y-10z+34=0$

$(2x-y-z)^2+(y^2-6y+9)+(z^2-10z+25)=0$
$(2x-y-z)^2+(y-3)^2+(z-5)^2=0$

Vì $(2x-y-z)^2\geq 0; (y-3)^2\geq 0; (z-5)^2\geq 0$ với mọi $x,y,z$

Do đó để tổng của chúng bằng $0$ thì bản thân mỗi số đó bằng $0$

$\Rightarrow 2x-y-z=y-3=z-5=0$

$\Rightarrow y=3; z=5; x=4$

Khi đó:
$P=0^{2023}+(-1)^{2025}+(5-4)^{2027}=0$

(\(x+y\)) = a; (\(x^3\) + y³) = b. 

 \(x^3\) + y³ = (\(x\) + y).(\(x^2\) - \(xy\) + y²) (1)

Thay \(x\) + y = a; \(x^3\) + y³ = b vào biểu thức (1) ta có:

 a.(\(x^2\) - \(xy\) + y²) =  b

     \(x^2\) - \(xy\) + y² = \(\dfrac{b}{a}\)

     \(x^2\) + 2\(xy\) + y² - 3\(xy\) = \(\dfrac{b}{a}\)

    (\(x+y\))² - 3\(xy\)           = \(\dfrac{b}{a}\)

         a² - 3\(xy\)               = \(\dfrac{b}{a}\)

               3\(xy\)                = a² - \(\dfrac{b}{a}\)

                \(xy\)                 = (\(a^2\) - \(\dfrac{b}{a}\)): 3

                \(xy\)               = \(\dfrac{a^3-b}{3a}\)

    Thay \(xy\) = \(\dfrac{a^3-b}{3a}\) vào biểu thức:

               \(x^2\) - \(xy\) + y² = \(\dfrac{b}{a}\) ta có 

                \(x^2\)  - \(\dfrac{a^3-b}{3a}\)+ y²  = \(\dfrac{b}{a}\)

                  \(x^2\) + y² = \(\dfrac{b}{a}\) + \(\dfrac{a^3-b}{3a}\)

                 \(x^2\)  + y² = \(\dfrac{3b+a^3-b}{3a}\)

                 \(x^2\) + y² = \(\dfrac{a^3+2b}{3a}\)

Bài 6: Ta có:

\(4x^2+2y^2+2z^2-4xy-4xz+2yz-6y-10z+34=0\)

\(\Leftrightarrow4x^2+y^2+z^2-4xy-4xz+2yz+y^2-6y+9+z^2-10z+25=0\)

\(\Leftrightarrow\left[\left(2x\right)^2+y^2+z^2-2\cdot2x\cdot y-2\cdot2x\cdot z+2\cdot y\cdot z\right]+\left(y^2-6y+9\right)+\left(z^2-10z+25\right)=0\)

\(\Leftrightarrow\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)

Mà: \(\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2\ge0\forall x,y,z\)

Mặt khác: \(\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-y-z=0\\y-3=0\\z-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-3-5=0\\y=3\\z=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x=8\\y=3\\z=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\\z=5\end{matrix}\right.\)

Thay vào S ta có:

\(S=\left(4-4\right)^{2023}+\left(3-4\right)^{2025}+\left(5-4\right)^{2027}=0-1+1=0\)