5 < x^3-15 < 16 Tìm các số nguyên x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét n = 5k;
=> 3n+2 = 15k + 2 (không chia hết cho 5)
xét n = 5k+1:
=> 3n+2 =15k+5(thỏa mãn)
Xét n = 5k+2:
=> 3n + 2 = 15k + 8 (không chia hết cho 5)
Xét n = 5k+3:
=> 3n+2 = 15k+11(không chia hết)
Xét n = 5k+4:
=> 3n+2 = 15k + 14(không chia hết)
Đáp số: n = 5k+1(k thuộc tập hợp N)

\(\dfrac{5}{3}\)+\(\dfrac{1}{4}\)-\(\dfrac{8}{3}\) - \(\dfrac{7}{4}\) + \(\dfrac{3}{2}\)
(\(\dfrac{5}{3}-\dfrac{8}{3}\))+(\(\dfrac{1}{4}-\dfrac{7}{4}\)) + \(\dfrac{3}{2}\)
= -1 - \(\dfrac{3}{2}\) + \(\dfrac{3}{2}\)
= -1

A = (\(x\) + 1)2022 + (\(\sqrt{y-1}\))2023 đkxđ : y - 1 ≥ 0 ⇒ y ≥ 1
⇔ (\(x\) + 1)2022 + (\(\sqrt{y-1}\))2023 = 0
vì (\(x\) + 1)2022 ≥ 0; \(\sqrt{y-1}\) ≥ 0 ⇒ (\(\sqrt{y-1}\))2023 ≥ 0
Nên A = 0 ⇔ \(\left\{{}\begin{matrix}x+1=0\\y-1=0\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Nghiệm của A là: \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)

Tìm GTNN chứ nhỉ e
\(D=\left|2022-x\right|+\left|x-1\right|\ge\left|2022-x+x-1\right|=2021\)
Dấu "=" xảy ra \(\Leftrightarrow\left(2022-x\right)\left(x-1\right)\ge0\)
\(\Leftrightarrow1\le x\le2022\)
Vậy Min D=2021 \(\Leftrightarrow1\le x\le2022\)

Độ dài cạnh CD hay AB là: \(480:30=16\left(cm\right)\)
Độ dài CE là: \(30.2=60\left(cm\right)\)
Độ dài cạnh AD hay BC là: \(480:60=8\left(cm\right)\)
Chu vi hình bình hành ABCD là: \(\left(16+8\right).2=48\left(cm\right)\)

`5x-5/6 =3x+2/3`
`=> 5x-3x=2/3+5/6`
`=>2x= 4/6 + 5/6`
`=> 2x= 9/6`
`=> x= 3/2 :2`
`=>x=3/2xx1/2`
`=>x= 3/4`
Vâỵ `x=3/4`
`@` `\text {Ans}`
`\downarrow`
`c)`
`5x - 5/6 = 3x + 2/3`
`=> 5x - 3x = 2/3 + 5/6`
`=> 2x = 3/2`
`=> x= 3/2 \div 2`
`=> x=3/4`

\(\dfrac{2^{15}+2^{10}}{2^{10}+2^5}=\dfrac{2^{10}\left(2^5+1\right)}{2^5\left(2^5+1\right)}=\dfrac{2^{10}}{2^5}=2^5=32\)
\(\dfrac{2^{15}+2^{10}}{2^{10}+2^5}\) = \(\dfrac{2^5\left(2^{10}+2^5\right)}{2^{10}+2^5}\) = 25 = 32
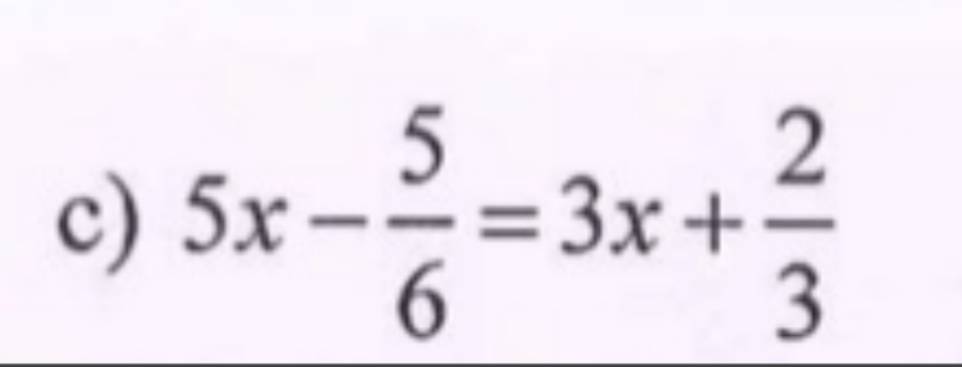
Dùng nguyên lý kẹp để tìm nghiệm nguyên em nhé .
5 < \(x^3\) - 15 < 16
5 + 15 < \(x^3\) < 16 + 15
20 < \(x^3\) < 31
⇒ 8 < \(x^3\) < 64
⇒ 23 < \(x^3\) < 43
Vì \(x\) là số nguyên nên \(x\) = 3