 Bài này làm sao vậy
Bài này làm sao vậy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$A=1-3+3^2-3^3+3^4-....+3^{38}-3^{39}$
$3A=3-3^2+3^3-3^4+3^5-...+3^{39}-3^{40}$
$A+3A=(1-3+3^2-3^3+3^4-....+3^{38}-3^{39})+(3-3^2+3^3-3^4+3^5-...+3^{39}-3^{40})$
$4A=1-3^{40}$
b.
Xét $B=1-3+3^2-3^3+....+3^{98}-3^{99}$
$3B=3-3^2+3^3-3^4+....+3^{99}-3^{100}$
$\Rightarrow B+3B=1-3^{100}$
$4B=1-3^{100}$
$3^{100}=1-4B$
Suy ra $3^{100}$ chia $4$ dư $1$

`(x+3)^3-1=31-2^2`
`(x+3)^3-1=31-4`
`(x+3)^3-1=27`
`(x+3)^3=27+1`
`(x+3)^3=28`
xem lại đề=)

Vì vòi 1 chảy 4h vòi 2 chảy 6h thì được \(\dfrac{2}{5}\) bể nên vòi 1 chảy \(4:\dfrac{2}{5}=10h\) vòi 2 chảy \(6:\dfrac{2}{5}=15\left(h\right)\) thì đầy bể.
Vòi 1 và vòi 2 chảy có tỉ lệ lần lượt là \(10:15\) hay \(2:3\)
Gọi thời gian mỗi vòi chảy đầy bể lần lượt là \(a,b\left(giờ\right)\)
Theo bài toán, ta có:
\(2a=3b\) hay \(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{1}{3}}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{1}{3}}=\dfrac{a+b}{\dfrac{1}{2}+\dfrac{1}{3}}=\dfrac{12}{\dfrac{5}{6}}=14,4\)
Từ đây suy ra:
\(a=\dfrac{1}{2}\cdot14,4=7,2\)
\(b=\dfrac{1}{3}\cdot14,4=4,8\)
Vậy vòi thứ nhất mất 7,2 giờ để đầy bể, vòi thứ hai mất 4,8 giờ để đầy bể.

dịch :
Điều tôi muốn sẽ trở thành sự thật
có thể nói là
Ước mơ của tôi sẽ trở thành sự thật. Cũng đc


đường kính hình tròn là
62,8:3,14=20(cm)
bán kính hình tròn là
20:2=10(cm)
vì ABCD là hình vuông nên nên => AC⊥BD => AO⊥BD
=> AO là chiều cao của tam giác ABD
\(S_{ABD}=AO\cdot BD\cdot\dfrac{1}{2}=20\cdot10\cdot\dfrac{1}{2}=100\left(cm^2\right)\)
c/m ta có \(S_{BCD}=100cm^2\)
có \(S_{ABCD}=S_{ABD}+S_{CBD}=100+100=200\left(cm^2\right)\)

mik nghĩ nó kiểu nhất mạnh câu v á
như chiếc áo rất đẹp biểu diễn chiếc áo ấy thật sự rất đẹp mik bt v thôi

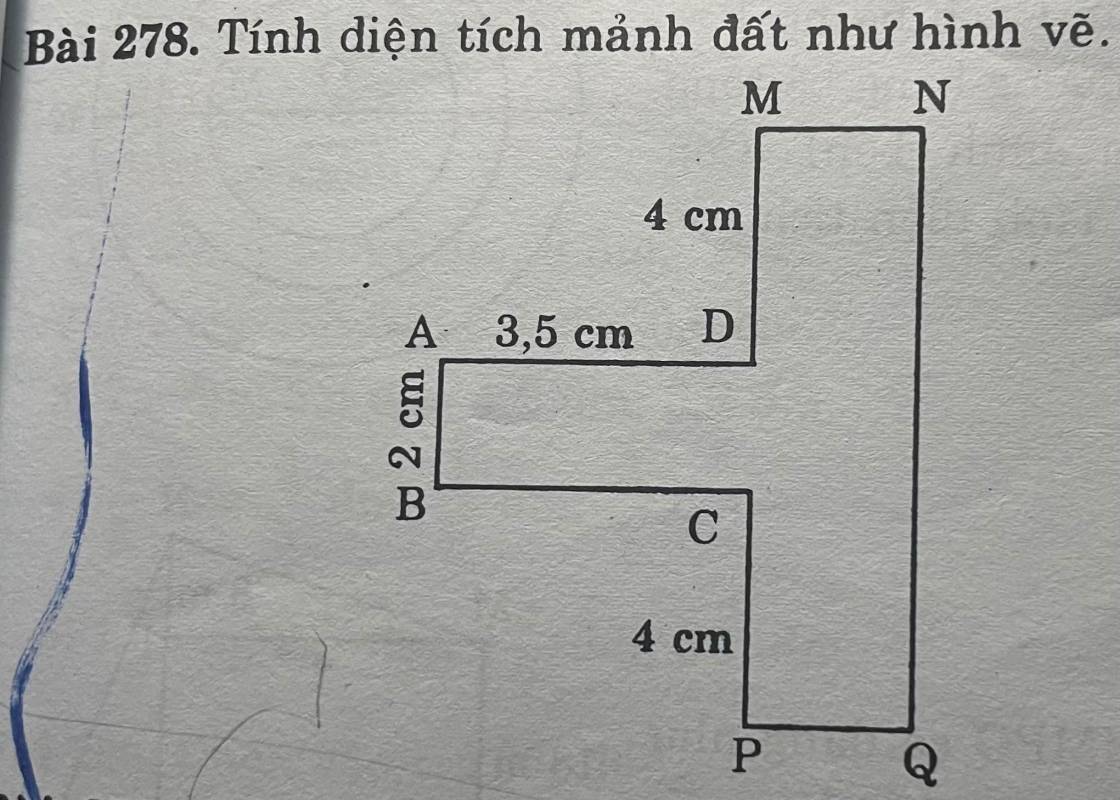
Thiếu dữ kiện về độ dài MN hoặc PQ nên diện tích hình trên không tính được bạn ạ.