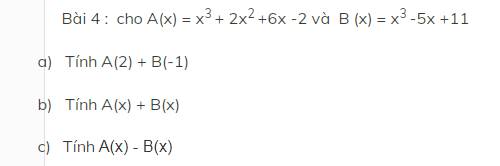
\(\left|x+3\right|-2x=\left|x-4\right|\)

\(\Rightarrow\left|x+3\right|=2x+\left|x-4\right|\)

\(\Rightarrow\left\{{}\begin{matrix}x+3=2x+\left|x-4\right|\left(\text{loại}\right)\\x+3=-2x-\left|x-4\right|\end{matrix}\right.\)

*Ta loại trường hợp trên vì không có x thỏa mãn, cách để suy ra không có trường hợp thỏa mãn với trường hợp trên tương tự với cách tìm giá trị thỏa mãn x mình làm ở trường hợp dưới.

\(\Rightarrow3x+3+\left|x-4\right|=0\)

\(\Rightarrow\left|x-4\right|=-3x-3\)

\(\Rightarrow\left\{{}\begin{matrix}x-4=-3x-3\\x-4=3x+3\end{matrix}\right.\)

Với hạng tử liên quan x chuyển qua trái, ngược lại chuyển sang phải (chuyển vế thì đổi dấu)

\(\Rightarrow\left\{{}\begin{matrix}x+3x=4-3\\x-3x=4+3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}4x=1\\-2x=7\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{4}\left(loại\right)\\x=-\dfrac{7}{2}\end{matrix}\right.\)

loại x=1/4 vì khi thay vào biểu thức đề không thỏa mãn

\(\Rightarrow x=-\dfrac{7}{2}\)

Thay lại tất cả ngoặc nhọn mình dùng thành ngoặc vuông nha bạn.

\(\left\{{}\begin{matrix}a\\b\end{matrix}\right.\rightarrow\left[{}\begin{matrix}a\\b\end{matrix}\right.\)

-1/5 : 1 2/5 = -2/7 : x

-1/5 : 7/5 = -2/7 : x

-1/7 = -2/7 : x

x = -2/7 : -1/7

x = 2

giúp mình với ạ

mình cần gấp

Lời giải:

$|x|=1\Rightarrow x^2=1$

$A=3x^2+2^y-1=3.1+2^{-1}-1=3+\frac{1}{2}-1=\frac{5}{2}$

Bafi4:

a; A(2) = 2³ + 2.2² + 6.2 -  2

   A(2) = 8 + 8 + 12 - 2

   A(2) = (8 + 12) + (8 - 2)

  A(2) =  20 + 6

  A(2) =  26

b; B(\(x\)) = \(x^3\) - 5.\(x\) + 11

    B(-1) = (-1)³ - 5.(-1) + 11

   B(-1) = -1 + 5 + 11

  B(-1) =  ( -1 + 11) + 5

  B(-1) =  10 + 5

  B(-1) = 15

b; A(\(x\)) + B(\(x\)) = \(x^3\) + 2.\(x^2\) + 6\(x\) - 2 + \(x^3\) - 5\(x\) + 11

    A(\(x\)) + B(\(x\)) = (\(x^3\) + \(x^3\)) + 2\(x^2\) + (6\(x\) - 5\(x\)) + (11 - 2)

   A(\(x\)) + B(\(x\)) = 2\(x^3\) + 2\(x^2\) + \(x\) + 9