\(x-4\sqrt{x-1}+3=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


nếu lần cuối không bán thêm 500 quả thì số trứng còn lại là:
600 + 500 = 1100 (quả)
phân số chỉ 1100 quả là :
1 - 1/2 = 1/2 (số trứng còn lại sau lần bán thứ hai)
số trứng còn lại sau lần bán thứ hai là:
1100 : 1/2 = 2200 (quả)
nếu lần bán thứ hai không bán thêm 400 quá thì số trứng còn lại là:
2200 + 400 = 2600 (quả)
phân số chỉ 2600 quả là:
1 - 1/3 = 2/3 (số trứng còn lại sau lần bán thứ nhất)
số trứng còn lại sau lần bán thứ nhất là: 2600 : 2/3 = 3900 (quả)
nếu lần bán thứ nhất không bán thêm 300 quả thì số trứng còn lại là:
3900 + 300 = 4200 (quả)
phân số chỉ 4200 quả là:
1 - 1/4 = 3/4 (số trứng)
số trứng cần bán là: 4200 : 3/4 = 5600 (quả)
đs....

ĐKXĐ : \(0\le x\le1\) ; \(\sqrt{x}+\sqrt{1-x}>0\)
Đặt \(\sqrt{x}=a;\sqrt{1-x}=b\left(a;b\ge0\right)\)
=> a2 + b2 = 1 (1)
Khi đó phương trình <=> \(\dfrac{2a^3}{a+b}+ab=1\)
<=> 2a3 + ab(a + b) = a + b
<=> 2a3 + a2b + ab2 - (a + b) = 0
<=> (a3 + a2b + ab2 + b3) - (a + b) + (a3 - b3) = 0
<=> (a + b)(a2 + b2 - 1) + a3 - b3 = 0 (2)
Kết hợp (1);(2) được a3 - b3 = 0
<=> a = b
<=> \(\sqrt{x}=\sqrt{1-x}\Leftrightarrow x=\dfrac{1}{2}\)(tm)
Vậy tập nghiệm \(S=\left\{\dfrac{1}{2}\right\}\)

xét A(0;1) ta có: 2.02 + 1 = 1 vậy A ϵ y = 2x2 + 1
xét B(-1,1) ta có : 2.(-1)2 + 1 = 3 vậy B \(\notin\) y = 2x2 + 1
xét C(1,3) ta có: 2.12 + 1 = 3 vậy C ϵ y = 2x2 + 1
xét D(-2,-4) ta có : 2.(-2)2 + 1 = 9 vậy D \(\notin\) y = 2x2 + 1
xét E(2,6) ta có : 2.22 + 1 = 9 vậy E \(\notin\) y = 2x2 + 1
Bạn thay lần lượt từng điểm vào nhé. Ví dụ A(0,1) ta thay x=0 vào đồ thị ta được kết quả y=1 => A thuộc đồ thị
Tương tự như vậy ta có điểm C(1;3) cũng thuộc đồ thị

\(Đk:x\ge0;y\ge1;z\ge2\)
\(\sqrt{x}+\sqrt{y-1}+\sqrt{z-2}=\dfrac{1}{2}\left(x+y+z\right)\)
\(\Leftrightarrow x+y+z-2\sqrt{x}-2\sqrt{y-1}-2\sqrt{z-2}=0\)
\(\Leftrightarrow\left[x-2\sqrt{x}+1\right]-1+\left[\left(y-1\right)-2\sqrt{y-1}+1\right]+\left[\left(z-2\right)-2\sqrt{z-2}+1\right]+1=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2+\left(\sqrt{y-1}-1\right)^2+\left(\sqrt{z-2}-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{x}-1\right)^2=0\\\left(\sqrt{y-1}-1\right)^2=0\\\left(\sqrt{z-2}-1\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\\z=3\end{matrix}\right.\)

\(a,=\sqrt{a}\left(\sqrt{b}-1\right)-\left(\sqrt{b}-1\right)\\ =\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)\\ b,=\sqrt{a}\left(\sqrt{a}+1\right)+2\sqrt{b}\left(\sqrt{a}+1\right)\\ =\left(\sqrt{a}+2\sqrt{b}\right)\left(\sqrt{a}+1\right)\\ c,Sửa:x\sqrt{x}+y\sqrt{y}+x+y\\ =\sqrt{xy}\left(x+y\right)+\left(x+y\right)=\left(\sqrt{xy}+1\right)\left(x+y\right)\\ d,=x+\sqrt{x}-2\sqrt{x}-2\\ =\sqrt{x}\left(\sqrt{x}+1\right)-2\left(\sqrt{x}+1\right)\\ =\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
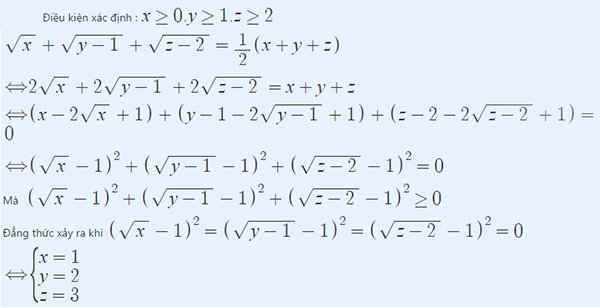
x - 4\(\sqrt{x-1}\) + 3 = 0
(\(\sqrt{x-1}\) )2 - 4\(\sqrt{x-1}\) + 4 = 0
△ = (-4)2 -4.4 = 0
\(\sqrt{x-1}\) = 2
x - 1 = 4
x = 5