TH1: p=2

\(p^2+8=2^2+8=12\) không là số nguyên tố

=>Loại

TH2: p=3

\(p^2+8=3^2+8=17\) là số nguyên tố

\(p^2+2=3^2+2=11\) là số nguyên tố

=>Nhận

TH3: p=3k+1

\(p^2+8=\left(3k+1\right)^2+8=9k^2+6k+9=3\left(3k^2+2k+3\right)⋮3\)

=>p^2+8 không là số nguyên tố

=>Loại

TH4: p=3k+2

\(p^2+8=\left(3k+2\right)^2+8\)

\(=9k^2+12k+4+8=9k^2+12k+12=3\left(3k^2+4k+4\right)⋮3\)

=>p^2+8 không là số nguyên tố

=>Loại

Vậy: p=3

\(-\dfrac{5}{7}\cdot\dfrac{2}{11}+\left(-\dfrac{5}{7}\right)\cdot\dfrac{4}{11}+\dfrac{5}{7}\cdot\left(-\dfrac{5}{11}\right)\\ =-\dfrac{5}{7}\cdot\dfrac{2}{11}+\left(-\dfrac{5}{7}\right)\cdot\dfrac{4}{11}+\left(-\dfrac{5}{7}\right)\cdot\dfrac{5}{11}\\ =\left(-\dfrac{5}{7}\right)\cdot\left(\dfrac{2}{11}+\dfrac{4}{11}+\dfrac{5}{11}\right)\\ =\left(-\dfrac{5}{7}\right)\cdot1=-\dfrac{5}{7}\)

\(\dfrac{5}{7}\cdot\dfrac{6}{13}-\left(-\dfrac{7}{13}\cdot\dfrac{5}{7}\right)+\dfrac{1}{7}:\dfrac{1}{2}\\ =\dfrac{5}{7}\cdot\dfrac{6}{13}-\left(-\dfrac{7}{13}\cdot\dfrac{5}{7}\right)+\dfrac{1}{7}\cdot2\\ =\dfrac{5}{7}\cdot\left[\dfrac{6}{13}-\left(-\dfrac{7}{13}\right)\right]+\dfrac{2}{7}\\ =\dfrac{5}{7}\cdot1+\dfrac{2}{7}=1\)

\(\left(2\dfrac{2}{15}\cdot\dfrac{9}{17}\cdot\dfrac{3}{32}\right):\left(-\dfrac{3}{17}\right)\\ =\left(\dfrac{32}{15}\cdot\dfrac{9}{17}\cdot\dfrac{3}{32}\right)\cdot\left(-\dfrac{17}{3}\right)\\ =\dfrac{32}{15}\cdot\dfrac{9}{17}\cdot\dfrac{3}{32}\cdot\dfrac{-17}{3}\\ =\left(\dfrac{32}{15}\cdot\dfrac{3}{32}\right)\cdot\left(\dfrac{9}{17}\cdot\dfrac{-17}{3}\right)\\ =\dfrac{1}{5}\cdot\left(-3\right)=-\dfrac{3}{5}\)

a) 

\(\dfrac{-5}{11}\cdot\dfrac{7}{15}\cdot\dfrac{11}{-5}\cdot\left(-30\right)\\ =\left(\dfrac{-5}{11}\cdot\dfrac{11}{-5}\right)\cdot\left(\dfrac{7}{15}\cdot-30\right)\\ =1\cdot-14\\ =-14\)

b) 

\(-\dfrac{1}{3}\cdot\left(-\dfrac{15}{19}\right)\cdot\dfrac{38}{45}\\ =-\dfrac{1}{3}\cdot\left(-\dfrac{15}{29}\cdot\dfrac{38}{45}\right)\\ =-\dfrac{1}{3}\cdot\left(-\dfrac{15}{29}\cdot\dfrac{2\cdot19}{3\cdot15}\right)\\ =-\dfrac{1}{3}\cdot-\dfrac{2}{3}\\ =\dfrac{2}{9}\)

\(9\left(x-1\right)^2-\left(x-1\right)^4=0\\ \Rightarrow\left(x-1\right)^2\left[9-\left(x-1\right)^2\right]\\ \Rightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\9-\left(x-1\right)^2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-1=0\\9=\left(x-1\right)^2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\3^2=x-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x-1=3\\x-1=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=4\\x=-2\end{matrix}\right.\) 

________________________

\(\left(2x-3\right)^2+2x=3\\ \Rightarrow\left(2x-3\right)^2+\left(2x-3\right)=0\\ \Rightarrow\left(2x-3\right)\left(2x-3+1\right)=0\\ \Rightarrow\left(2x-3\right)\left(2x-2\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x-3=0\\2x-2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x=3\\2x=2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{2}{2}=1\end{matrix}\right.\)

đừng đăng linh tinh nhé bạn (Phạm Minh Khuê)
 

Chào các bạn đã kết bạn với tớ, các bạn có khỏe mạnh không, giờ tớ đang học nè, còn các cậu đang làm gì. 

a; Áp dụng công thức:

     \(\dfrac{a}{b}\) > \(\dfrac{a+m}{b+m}\) (a; b; m \(\in\) N' a > b)

Ta có: \(\dfrac{999}{556}\) > \(\dfrac{999+1}{556+1}\) = \(\dfrac{1000}{557}\)

b; \(\dfrac{-2}{15}\) < 0

   \(\dfrac{-10}{-11}\) = \(\dfrac{-10:-1}{-11:-1}\) = \(\dfrac{10}{11}\) > 0

\(\dfrac{-2}{15}\) < 0 < \(\dfrac{-10}{-11}\)

 Vậy \(\dfrac{-2}{15}\) < \(\dfrac{-10}{-11}\)

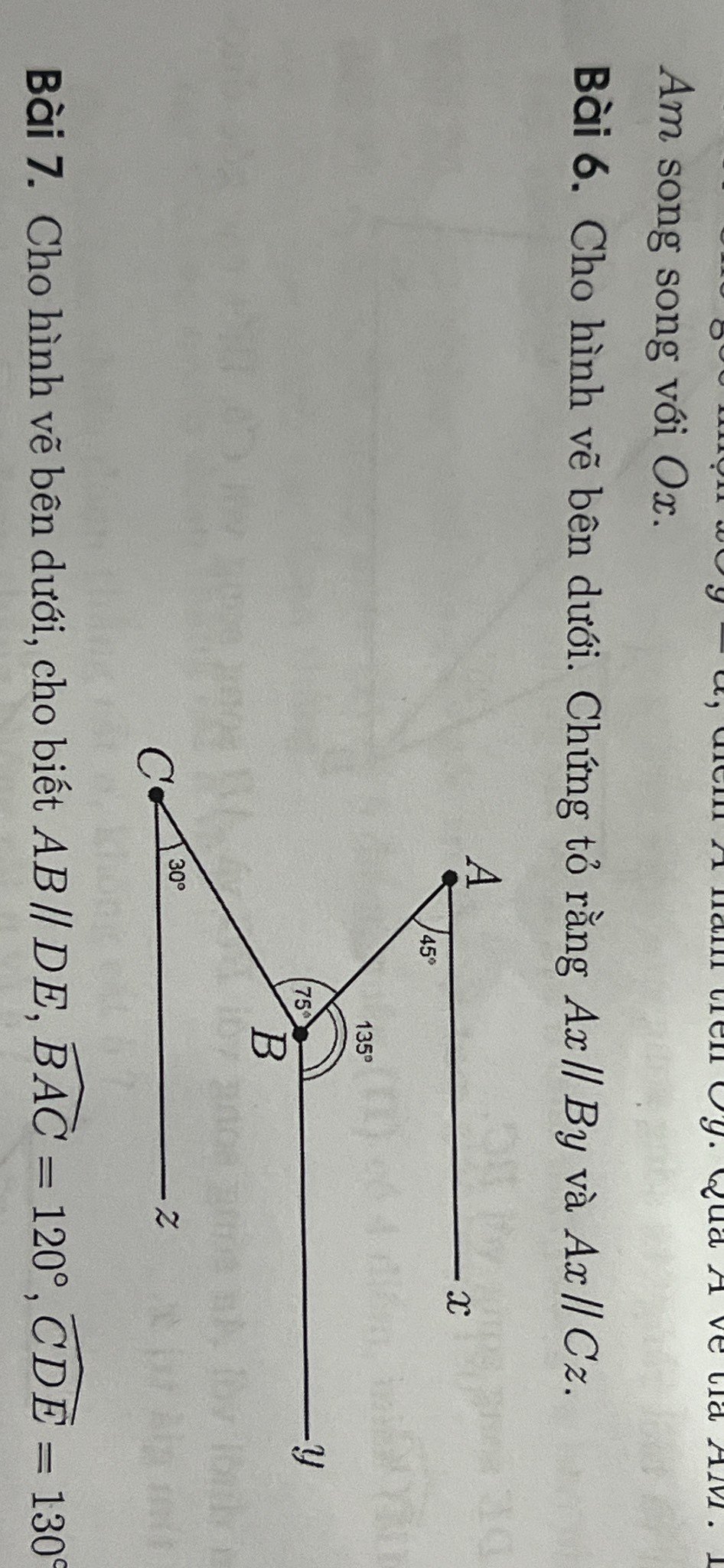
\(\widehat{xAB}+\widehat{ABy}=45^o+135^o=180^o\)

Mà 2 góc này ở vị trí trong cùng phía 

⇒ Ax//By (1)

\(\widehat{CBA}+\widehat{CBy}+\widehat{ABy}=360^o\)

\(\Rightarrow\widehat{CBy}=360^o-135^o-75^o=150^o\)

\(\widehat{BCz}+\widehat{CBy}=30^o+150^o=180^o\)

Mà 2 góc này ở vị tri trong cùng phia 

⇒ By//Cz (2)

Từ (1) và (2) => Ax//Cz