cho biểu thức:B=x+12/căn x +2.Chứng minh B lớn hơn bằng 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình nghĩ phải là \(HB.HC=4OE^2\) mới đúng.
Dễ thấy tứ giác AEHF là hình chữ nhật do có \(\widehat{EAF}=\widehat{AEH}=\widehat{AFH}=90^o\)
Do đó \(EF=AH\) (2 đường chéo của hình chữ nhật thì bằng nhau) và \(AH=EF=2OE\) (do 2 đường chéo của hình chữ nhật cắt nhau tại trung điểm mỗi đoạn)
Tam giác ABC vuông tại A có đường cao AH nên \(HB.HC=AH^2\) \(\Rightarrow HB.HC=\left(2OE\right)^2=4OE^2\) (đpcm)

giá một quyển vở là 448000: 56 = 8000 (đồng)
số tiền Minh mua vở là (448000+32000): 2 = 240000(đồng)
số vở Minh đã mua là 240000: 8000 = 30 (quyển)
số vở Thảo đã mua là 56 - 30 = 26 (quyển)
đs...

\(S_{ABCD}=\dfrac{1}{2}AC.\left(AB+AD\right)\)
Nếu ta đặt đọ dài cạnh AB=a
tam giác ABC vuông tại A có góc B=600 nên nếu gọi AB=a thì \(AC=\sqrt{3}a\)
ta lại xét tam giác ADC vuông tại D có góc ACD dễ tính bằng 30 độ
bạn sẽ lại có:
\(AD=\dfrac{1}{2}AC=\dfrac{\sqrt{3}a}{2}\) đây là T/C của tam giác vuông có 1 góc = 30 độ
như vậy:
\(S_{ABCD}=\dfrac{1}{2}\sqrt{3}a.\left(a+\dfrac{\sqrt{3}a}{2}\right)=\dfrac{1}{2}a^2.\left(\sqrt{3}+\dfrac{1}{2}\right)\)
trong đó a=AB


Lời giải:
Minh mua 20 cuốn tập hết số tiền là:
$10 000\times 20=200000$ (đồng)
Minh mua 5 cây viết hết số tiền là:
$240000-200000=40000$ (đồng)
Giá tiền một cây viết là:
$40000:5=8000$ (đồng)
Số tiền mua 20 cuốn tập là:
\(20.10000=200000\) ( đồng )
Số tiền mua 5 cây viết là:
\(240000-200000=40000\) ( đồng )
Số tiền mua 1 cây viết là:
\(40000:5=8000\) ( đồng )
Đ/s:.....

các số có hai chữ số là 10; 11; 12; .....99
A = 10 + 11 + 12 + ....+ 99
A = (10 + 99){ ( 99-10): 1+1} : 2 = 4905
các số có hai chữ số chia hết cho 7 là 14; 21;....;98
B = 14 + 21 + ....+ 98
B = (14+ 98){ ( 98- 14): 7 + 1 }: 2 = 728
tổng các số có hai chữ số không chia hết cho bảy là
A - B = 4905 - 728 =4177
đs....
Các số chia hết cho 7 là :14,21,28,35,42,49,56,63,70,77,84,91,98.
Tổng của các số đó là :(98+14).13/2=728

các số có hai chữ số là 10; 11; 12; .....99
A = 10 + 11 + 12 + ....+ 99
A = (10 + 99){ ( 99-10): 1+1} : 2 = 4905
các số có hai chữ số chia hết cho 7 là 14; 21;....;98
B = 14 + 21 + ....+ 98
B = (14+ 98){ ( 98- 14): 7 + 1 }: 2 = 728
tổng các số có hai chữ số không chia hết cho bảy là
A - B = 4905 - 728 =4177
đs....
các số có hai chữ số là 10; 11; 12; .....99
A = 10 + 11 + 12 + ....+ 99
A = (10 + 99){ ( 99-10): 1+1} : 2 = 4905
các số có hai chữ số chia hết cho 7 là 14; 21;....;98
B = 14 + 21 + ....+ 98
B = (14+ 98){ ( 98- 14): 7 + 1 }: 2 = 728
tổng các số có hai chữ số không chia hết cho bảy là
A - B = 4905 - 728 =4177
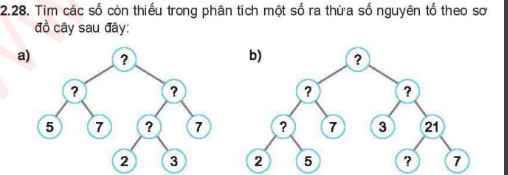 bài này lm kiểu j tui mới "lớp 1"
bài này lm kiểu j tui mới "lớp 1"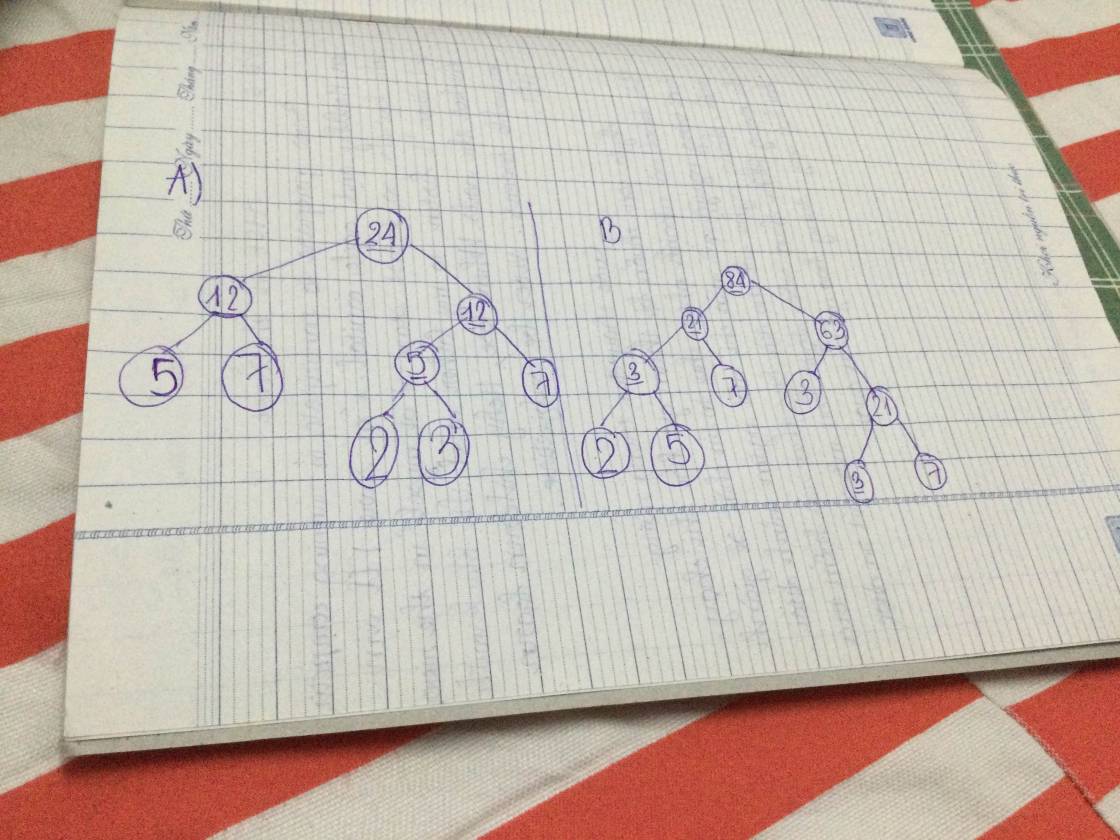
\(B=\dfrac{x+12}{\sqrt{x}+2}\) (điều kiện \(x\ge0\))
Đặt \(\sqrt{x}=t\left(t\ge0\right)\), khi đó \(B=\dfrac{t^2+12}{t+2}\) \(\Rightarrow\left(t+2\right)B=t^2+12\) \(\Leftrightarrow t^2-B.t+12-2B=0\) (*)
Phương trình (*) có \(\Delta=\left(-B\right)^2-4.1.\left(12-2B\right)\) \(=B^2+8B-48\)
Để pt (*) có nghiệm thì \(\Delta\ge0\) hay \(B^2+8B-48\ge0\) \(\Leftrightarrow\left(B+12\right)\left(B-4\right)\ge0\)
Ta xét 2 trường hợp:
TH1: \(\left\{{}\begin{matrix}B+12\ge0\\B-4\ge0\end{matrix}\right.\Leftrightarrow B\ge4\)
TH2: \(\left\{{}\begin{matrix}B+12\le0\\B-4\le0\end{matrix}\right.\Leftrightarrow B\le-12\)
Ta thấy do \(x\ge0\) nên \(x+12>0\) và \(\sqrt{x}+2>0\). Do đó \(B>0\). Vậy trường hợp 2 \(\left(B\le-12\right)\) là không thể xảy ra. Vậy ta chỉ nhận trường hợp \(B\ge4\) hay \(min_B=4\)
Khi \(B=4\) thì thay vào (*), ta có \(t^2-4t+12-2.4=0\) \(\Leftrightarrow t^2-4t+4=0\) \(\Leftrightarrow\left(t-2\right)^2=0\) \(\Leftrightarrow t=2\) (nhận)
\(\Leftrightarrow\sqrt{x}=2\) \(\Leftrightarrow x=4\) (nhận)
Vậy \(B\ge4\). Dấu "=" xảy ra khi \(x=4\)