Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{\left(a+b+a+c\right)^2}\le\dfrac{1}{4\left(a+b\right)\left(a+c\right)}=\dfrac{1}{4\left(a^2+ab+bc+ca\right)}\le\dfrac{1}{64}\left(\dfrac{1}{a^2}+\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}\right)\)
\(\le\dfrac{1}{64}\left(\dfrac{1}{a^2}+\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)=\dfrac{1}{64}\left(\dfrac{2}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\)
Tương tự và cộng lại:
\(P\le\dfrac{1}{64}\left(\dfrac{4}{a^2}+\dfrac{4}{b^2}+\dfrac{4}{c^2}\right)=\dfrac{1}{16}.3=\dfrac{3}{16}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Áp dụng bđt: \(\dfrac{1}{x+y}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(1\right)\)
\(\dfrac{1}{2a+b+c}=\dfrac{1}{\left(a+b\right)+\left(a+c\right)}\le\dfrac{1}{4}\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)\)
\(\Rightarrow P\le\dfrac{1}{16}\left[\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}\right)^2+\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}\right)^2+\left(\dfrac{1}{b+c}+\dfrac{1}{a+c}\right)^2\right]\)\(\Rightarrow16P\le\dfrac{2}{\left(a+b\right)^2}+\dfrac{2}{\left(b+c\right)^2}+\dfrac{2}{\left(a+c\right)^2}+\dfrac{2}{\left(a+b\right)\left(b+c\right)}+\dfrac{2}{\left(a+b\right)\left(b+c\right)}+\dfrac{2}{\left(b+c\right)\left(c+a\right)}\)
Áp dụng: \(x^2+y^2+z^2\ge xy+yz+xz\left(2\right)\) với a+b=x,b+c=y,c+a=z
\(\Rightarrow16P\le\dfrac{4}{\left(a+b\right)^2}+\dfrac{4}{\left(b+c\right)^2}+\dfrac{4}{\left(c+a\right)^2}\)
Ta có: \(\dfrac{1}{\left(a+b\right)^2}\le4.16.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2\)(do (1))
\(\Rightarrow16P\le\dfrac{1}{4}.16\left[\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\left(\dfrac{1}{b}+\dfrac{1}{c}\right)^2+\left(\dfrac{1}{c}+\dfrac{1}{a}\right)^2\right]=\dfrac{1}{4}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ca}\right)\le\dfrac{1}{4}.4.\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)=3\)(do(2) và \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=3\))
\(\Rightarrow P\le\dfrac{3}{16}\)
\(ĐTXR\Leftrightarrow a=b=c=1\)

\(\dfrac{\sqrt{b^2+a^2+a^2}}{ab}\ge\dfrac{\sqrt{\dfrac{1}{3}\left(b+a+a\right)^2}}{ab}=\dfrac{1}{\sqrt{3}}\left(\dfrac{1}{a}+\dfrac{2}{b}\right)\)
Tương tự: \(\dfrac{\sqrt{c^2+2b^2}}{bc}\ge\dfrac{1}{\sqrt{3}}\left(\dfrac{1}{b}+\dfrac{2}{c}\right)\) ; \(\dfrac{\sqrt{a^2+2c^2}}{ac}\ge\dfrac{1}{\sqrt{3}}\left(\dfrac{1}{c}+\dfrac{2}{a}\right)\)
Cộng vế với vế:
\(VT\ge\dfrac{1}{\sqrt{3}}\left(\dfrac{3}{a}+\dfrac{3}{b}+\dfrac{3}{c}\right)=\sqrt{3}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=1980\sqrt{3}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{3}{1980}\)

\(\sqrt{\dfrac{ab+2c^2}{1+ab-c^2}}=\sqrt{\dfrac{ab+2c^2}{a^2+b^2+ab}}\)\(=\dfrac{ab+2c^2}{\sqrt{\left(a^2+b^2+ab\right)\left(ab+c^2+c^2\right)}}\)\(\ge\dfrac{2\left(ab+2c^2\right)}{a^2+b^2+2ab+2c^2}\)\(\ge\dfrac{2\left(ab+2c^2\right)}{2\left(a^2+b^2\right)+2c^2}\)\(=\dfrac{ab+2c^2}{a^2+b^2+c^2}\)
\(\Rightarrow\sqrt{\dfrac{ab+2c^2}{1+ab-c^2}}\ge ab+2c^2\)
Tương tự: \(\sqrt{\dfrac{bc+2a^2}{1+bc-a^2}}\ge bc+2a^2\); \(\sqrt{\dfrac{ac+2b^2}{1+ac-b^2}}\ge ac+2b^2\)
Cộng vế với vế \(\Rightarrow VT\ge2a^2+2b^2+2c^2+ab+bc+ac=2+ab+bc+ac\)
Dấu = xảy ra khi \(a=b=c=\dfrac{1}{\sqrt{3}}\)

\(\dfrac{a^2b^2}{2a^2+b^2+3a^2b^2}=\dfrac{a^2b^2}{\left(a^2+b^2\right)+\left(a^2+a^2b^2\right)+2a^2b^2}\le\dfrac{a^2b^2}{2ab+2a^2b+2a^2b^2}=\dfrac{ab}{2\left(1+a+ab\right)}\)
Tương tự và cộng lại;
\(P\le\dfrac{1}{2}\left(\dfrac{ab}{1+a+ab}+\dfrac{bc}{1+b+bc}+\dfrac{ca}{1+c+ca}\right)\)
\(P\le\dfrac{1}{2}\left(\dfrac{ab}{1+a+ab}+\dfrac{abc}{a+ab+abc}+\dfrac{ab.ca}{ab+abc+ab.ca}\right)\)
\(P\le\dfrac{1}{2}\left(\dfrac{ab}{1+a+ab}+\dfrac{1}{a+ab+1}+\dfrac{a}{ab+1+a}\right)=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Ta có : \(a+b+c=3\Rightarrow a^2+b^2+c^2\ge3\)
Theo BĐT AM - GM ta có :
\(a^4+b^2\ge2a^2b\)
\(b^4+c^2\ge2b^2c\)
\(c^4+a^2\ge2c^2a\)
\(2a^2b^2+2a^2\ge4a^2b\)
\(2b^2c^2+2b^2\ge4b^2c\)
\(2c^2a^2+2c^2\ge4c^2a\)
Cộng từng vế BĐT ta được :
\(\left(a^2+b^2+c^2\right)^2+3\left(a^2+b^2+c^2\right)\ge6\left(a^2b+b^2c+c^2a\right)\)
\(\Rightarrow a^2b+b^2c+c^2a\le\dfrac{3^2+3^2}{6}=3\)
Theo BĐT Cauchy schwarz dưới dạng en-gel ta có :
\(VT\ge\dfrac{9}{6+a^2b+b^2c+c^2a}=\dfrac{9}{9}=1\)
Dấu bằng xảy ra khi \(a=b=c=1\)
Viết lại BĐT:\(\dfrac{a^2b}{a^2b+2}+\dfrac{b^2c}{b^2c+2}+\dfrac{c^2a}{c^2a+2}\le1\)
Áp dụng BĐT AM-GM:
\(VT\le\sum\dfrac{a^2b}{3\sqrt[3]{a^4b^2}}=\dfrac{1}{3}\left(\sqrt[3]{a^2b}+\sqrt[3]{b^2c}+\sqrt[3]{c^2a}\right)\)
\(\le\dfrac{1}{9}\left(3a+3b+3c\right)=1\)
Suy ra đpcm

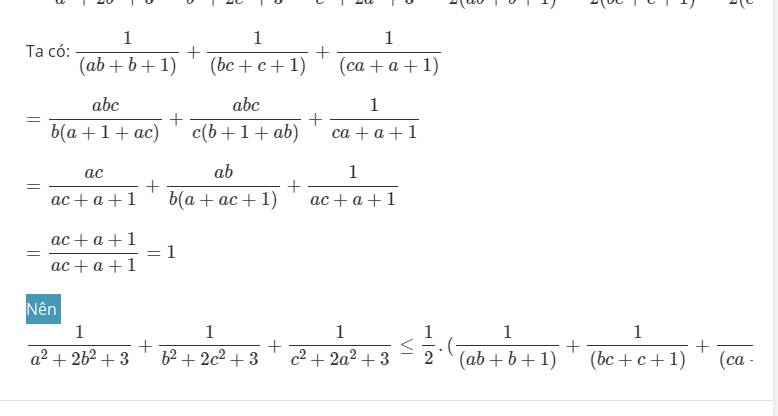



Áp dụng bất đẳng thức Cauchy-Schwarz ta có:
\(\dfrac{1}{2a^2+b^2}=\dfrac{1}{a^2+a^2+b^2}\le\dfrac{1}{9}\left(\dfrac{1}{a^2}+\dfrac{1}{a^2}+\dfrac{1}{b^2}\right)\)
\(\left\{{}\begin{matrix}\dfrac{1}{2b^2+c^2}\le\dfrac{1}{9}\left(\dfrac{1}{b^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\\\dfrac{1}{2c^2+a^2}\le\dfrac{1}{9}\left(\dfrac{1}{c^2}+\dfrac{1}{c^2}+\dfrac{1}{a^2}\right)\end{matrix}\right.\)
Cộng theo vế:
\(L\le\dfrac{1}{9}\left(\dfrac{3}{a^2}+\dfrac{3}{b^2}+\dfrac{3}{c^2}\right)=\dfrac{1}{9}\left[3\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\right]=\dfrac{1}{9}\)