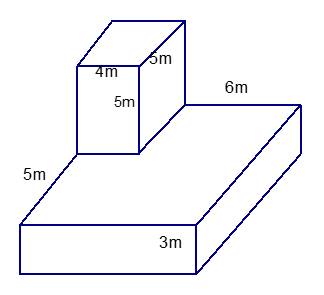
Tính thể tích của một khối bê tông gồm hai hình lăng trụ đứng tứ giác có kích thước như hình vẽ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để xác định xem 3n+10 có chia hết cho 2n+1 hay không, ta có thể sử dụng phép chia và kiểm tra phần dư. Nếu phần dư bằng 0, tức là 3n+10 chia hết cho 2n+1.
theo đề bài ta có:(3n+10) chia hết cho (2n+1)
(2n+1) chia hết cho (2n+1)
suy ra:{[2(3n+10)]-[3(2n+1)]} chia hết cho (2n+1)
hay 17 chia hết cho (2n+1)
suy ra: 2n+1 e Ư(17)
Ư(17)={1;17}
2n+1=1 thì n=0
2n+1=17 thì n=8
vậy n e {0;8}

\(20-\left[30-\left(5-1\right)^2\right]\)
\(=20-\left(30-4^2\right)\)
\(=20-\left(30-16\right)\)
\(=20-14\)
\(=6\)

\(2^3\cdot17-2^3\cdot14\)
\(=2^3\cdot\left(17-14\right)\)
\(=2^3\cdot3\)
\(=8\cdot3\)
\(=24\)

\(17\cdot85+15\cdot17-120\)
\(=17\cdot\left(85+15\right)-120\)
\(=17\cdot100-120\)
\(=1700-120\)
\(=1580\)

\(\left(2+4+6+...+2n\right)-53=103\)
\(\Rightarrow\left[\left(2n-2\right):2+1\right]\cdot\left(2n+2\right):2-53=103\)
\(\Rightarrow\left[2\left(n-1\right):2+1\right]\cdot\left(2n+2\right):2=103+53\)
\(\Rightarrow\left(n-1+1\right)\cdot2\cdot\left(n+1\right):2=156\)
\(\Rightarrow n\cdot\left(n+1\right)=156\)
\(\Rightarrow n\cdot\left(n+1\right)=12\cdot13\)
\(\Rightarrow n=12\)
Vậy: n = 12

\(3^{5n+2}+3^{5n+1}-3^{5n}=3^{5n}\left(3^2+3-1\right)=11.3^{5n}⋮11\)

x + 5 chia hết cho x + 3
⇒ x + 3 + 2 chia hết cho x + 3
⇒ x + 3 chia hết cho x + 3 và 2 chia hết cho x + 3
⇒ x + 3 ∈ Ư(2)
Mà: Ư(2) = {1; -1; 2; -2}
⇒ x + 3 ∈ {1; -1; 2; -2}
⇒ x ∈ {-2; -4; -1; -5}

\(a,x+39=50\\ \Rightarrow x=11\\ b,2x-15=17\\ \Rightarrow2x=32\\ \Rightarrow x=16.\)