Cho tam giác ABC vuông tại A có góc B = 60 độ . Trên BC lấy điểm H sao cho HB = AB , từ H kẻ HE vuông góc với BC tại H ( E thuộc AC) a) Tính góc C . b) Chứng minh BE là tia phân giác của góc B . c) Gọi K là giao điểm của BA và HE . Chứng minh rằng BE vuông góc với KC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề; BA=BM
Xét ΔBAN và ΔBMN có
BA=BM
\(\widehat{ABN}=\widehat{MBN}\)
BN chung
Do đó: ΔBAN=ΔBMN
=>\(\widehat{BAN}=\widehat{BMN}\)
=>\(\widehat{BMN}=90^0\)
=>NM\(\perp\)BC
Xét ΔNAD vuông tại A và ΔNMC vuông tại M có
NA=NM(ΔBAN=ΔBMN)
\(\widehat{AND}=\widehat{MNC}\)(hai góc đối đỉnh)
Do đó: ΔNAD=ΔNMC
=>AD=MC
BC=BM+MC
mà BA=BM và MC=AD
nên BC=BA+AD


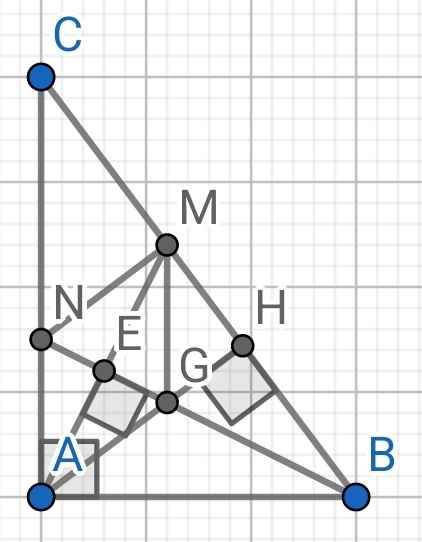
a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:
BA = BM (gt)
BE là cạnh chung
⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)
b) Do ∆ABE = ∆MBE (cmt)
⇒ ∠ABE = ∠MBE (hai góc tương ứng)
⇒ ∠ABN = ∠MBN
Xét ∆ABN và ∆MBN có:
BA = BM (gt)
∠ABN = ∠MBN (cmt)
BN là cạnh chung
⇒ ∆ABN = ∆MBN (c-g-c)
⇒ AN = MN (hai cạnh tương ứng)
c) Do ∆ABN = ∆MBN (cmt)
⇒ ∠BAN = ∠BMN (hai góc tương ứng)
Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ∠BMN = 90⁰
⇒ MN ⊥ BM
⇒ MN ⊥ BC
Lại có AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
Mà MN ⊥ BC (cmt)
⇒ AH // MN
⇒ ∠MGN = ∠ANG (so le trong)

a: \(A\left(x\right)=-2x^5+3x^2-4x^5+x^6-2x^2-1\)
\(=x^6+\left(-2x^5-4x^5\right)+\left(3x^2-2x^2\right)-1\)
\(=x^6-6x^5+x^2-1\)
\(=-1+x^2-6x^5+x^6\)
\(B\left(x\right)=-x^6+3-2x-x^2+x^4-2x^6-x^2+4x^2-x^4\)
\(=\left(-x^6-2x^6\right)+\left(x^4-x^4\right)+\left(-x^2-x^2+4x^2\right)-2x+3\)
\(=-3x^6+2x^2-2x+3\)
\(=3-2x+2x^2-3x^6\)
b: \(A\left(x\right)=x^6-6x^5+x^2-1\)
Hệ số cao nhất là 1
Hệ số tự do là -1
Bậc là 6
\(B\left(x\right)=-3x^6+2x^2-2x+3\)
Bậc là 6
Hệ số cao nhất là -3
Hệ số tự do là 3
c: \(A\left(-1\right)=\left(-1\right)^6-6\cdot\left(-1\right)^5+\left(-1\right)^2-1\)
=1+6+1-1
=7
\(A\left(0\right)=0^6-6\cdot0^5+0^2-1=-1\)
\(A\left(1\right)=1^6-6\cdot1^5+1^2-1=1-6+1-1=-5\)
\(A\left(2\right)=2^6-6\cdot2^5+2^2-1=64-192+4-1=68-193=-125\)
d: A(0)=-1
=>x=0 không là nghiệm của A(x)
\(B\left(1\right)=-3\cdot1^6+2\cdot1^2-2\cdot1+3\)
=-3+2-2+3
=0
=>x=1 là nghiệm của B(x)

Gọi số vở lớp 7A,7B,7C quyên góp lần lượt là a(quyển),b(quyển),c(quyển)
(ĐIều kiện: \(a,b,c\in Z^+\))
Số vở lớp 7A;7B;7C quyên góp lần lượt tỉ lệ với 2;3;4
=>\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
Tổng số vở 3 lớp quyên góp là 360 quyển nên a+b+c=360
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{360}{9}=40\)
=>\(a=40\cdot2=80;b=40\cdot3=120;c=40\cdot4=160\)
Vậy: số vở lớp 7A,7B,7C quyên góp lần lượt là 80(quyển),120(quyển),160(quyển)

Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
=>\(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC

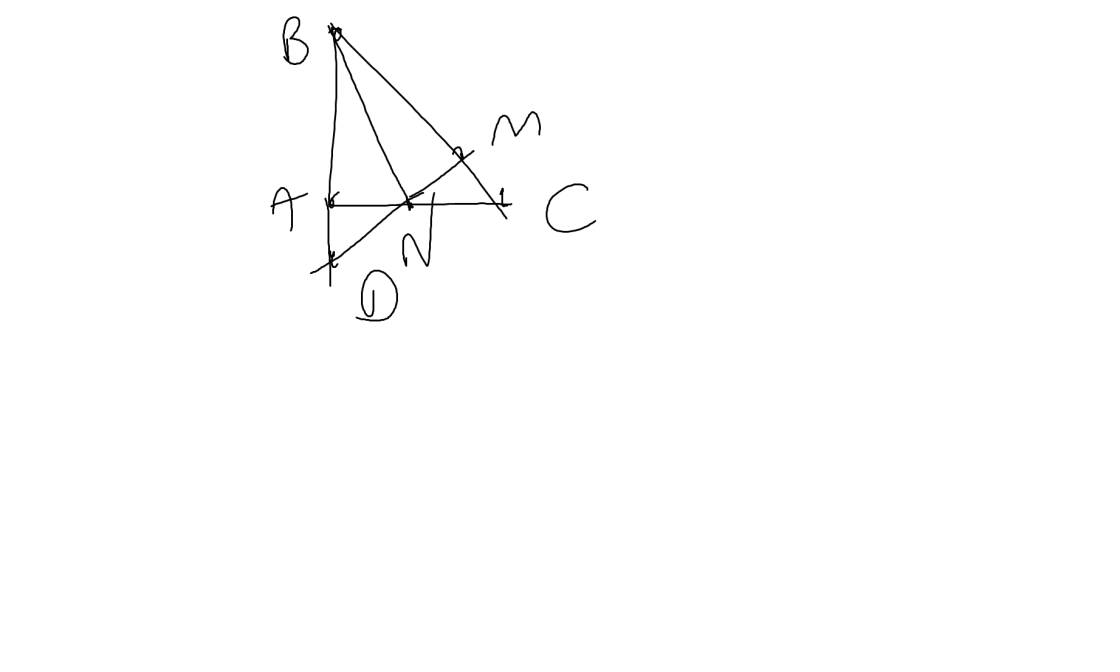





a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-60^0=30^0\)
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
Do đó: ΔBAE=ΔBHE
=>\(\widehat{ABE}=\widehat{HBẺ}\)
=>BE là phân giác của góc ABC
c: Xét ΔBKC có
KH,CA là các đường cao
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC
=>BE\(\perp\)KC
a) Tính góc C: Vì tam giác ABC vuông tại A và góc B = 60 độ, ta có góc C = 90 - 60 = 30 độ.
b) Chứng minh BE là tia phân giác của góc B: Gọi I là trung điểm của AB, vậy BI là đoạn thẳng phân giác của góc B. Ta có HB = AB và BI là đoạn thẳng phân giác của góc B, do đó tam giác BHI là tam giác đều. Do đó, góc BHI = 60 độ. Mà góc HBE là góc ngoài của tam giác BHI, vậy góc HBE = 60 độ. Vậy, BE là tia phân giác của góc B.
c) Chứng minh rằng BE vuông góc với KC: Ta có:
Vậy góc HKB = 90 độ.
Nhưng ta đã chứng minh BE là tia phân giác của góc B, vậy góc HBE = góc EBK.
Vậy ta có: góc EBK + góc HKB = góc HBE + góc HKB = 60 + 90 = 150 độ.
Nhưng tổng các góc trong tam giác BKH là 180 độ, vậy góc EBK + góc HKB = 180 độ.
Từ đó suy ra góc EBK = 30 độ.