Tìm n biết n thuộc tập hợp Z sao cho n+2/n+1 là một số nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


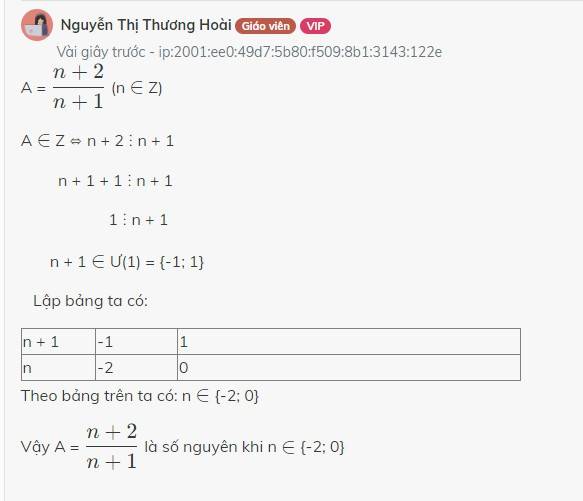
A = \(\dfrac{n+2}{n+1}\) (n \(\in\) Z)
A \(\in\) Z ⇔ n + 2 ⋮ n + 1
n + 1 + 1 ⋮ n + 1
1 ⋮ n + 1
n + 1 \(\in\) Ư(1) = {-1; 1}
Lập bảng ta có:
| n + 1 | -1 | 1 |
| n | -2 | 0 |
Theo bảng trên ta có: n \(\in\) {-2; 0}
Vậy A = \(\dfrac{n+2}{n+1}\) là số nguyên khi n \(\in\) {-2; 0}


Lời giải:
Với $n$ nguyên, để $\frac{n+2}{n+1}$ là số nguyên thì:
$n+2\vdots n+1$
$\Rightarrow (n+1)+1\vdots n+1$
$\Rightarrow 1\vdots n+1$
$\Rightarrow n+1\in\left\{1; -1\right\}$
$\Rightarrow n\in\left\{0; -2\right\}$

ĐKXĐ: n<>-1
Để \(\dfrac{n+2}{n+1}\) là số nguyên thì \(n+2⋮n+1\)
=>\(n+1+1⋮n+1\)
=>\(1⋮n+1\)
=>\(n+1\in\left\{1;-1\right\}\)
=>\(n\in\left\{0;-2\right\}\)

Lời giải:
Khi tăng chiều dài svđ lên 20% thì chiều dài mới bằng $100+20=120$ % chiều dài cũ
Khi tăng chiều rộng lên 25% thì chiều rộng mới bằng $100+25=125$ % chiều rộng cũ
Diện tích mới bằng:
$120.125:100=150$ (%) diện tích cũ
Diện tích cũ là:
$300:150\times 100=200$ (m2)
Lời giải:
Khi tăng chiều dài svđ lên 20% thì chiều dài mới bằng \(100 + 20 = 120\) % chiều dài cũ
Khi tăng chiều rộng lên 25% thì chiều rộng mới bằng \(100 + 25 = 125\) % chiều rộng cũ
Diện tích mới bằng:
\(120.125 : 100 = 150\) (%) diện tích cũ
Diện tích cũ là:
\(300 : 150 \times 100 = 200\) (m2)

Câu 4:
a: Các điểm là M,N,P
Đường thẳng là MN,NP,MP,xy
Các tia là Mx,My,Nx,Ny,Px,Py
b: N nằm trên các tia My, Px, Nx,Ny
Nx và My không phải là hai tia đối nhau vì chúng không có chung gốc
c: Theo hình vẽ, ta có: N nằm giữa M và P
=>MN+NP=MP
=>NP+3=8
=>NP=5(cm)
Câu 3:
a: Số học sinh giỏi là \(40\cdot\dfrac{1}{4}=10\left(bạn\right)\)
Số học sinh còn lại là 40-10=30(bạn)
Số học sinh trung bình là \(30\cdot\dfrac{3}{5}=18\left(bạn\right)\)
Số học sinh khá là 30-18=12(bạn)
b: Số học sinh khá chiếm:
\(\dfrac{12}{40}=30\%\)
Câu 2:
a: x+5,02=7,02
=>x=7,02-5,02
=>x=2
b: \(\dfrac{1}{2}x+\dfrac{7}{10}=\dfrac{3}{5}\)
=>\(\dfrac{1}{2}x=\dfrac{3}{5}-\dfrac{7}{10}=\dfrac{-1}{10}\)
=>\(x=-\dfrac{1}{10}\cdot2=-\dfrac{1}{5}\)
c: ĐKXĐ: x<>0
\(\dfrac{3}{x}=\dfrac{x}{27}\)
=>\(x\cdot x=3\cdot27=81\)
=>\(x^2=81\)
=>\(\left[{}\begin{matrix}x=9\left(nhận\right)\\x=-9\left(nhận\right)\end{matrix}\right.\)

Số tiền Lan mua bút là :
\(150.\dfrac{1}{5}=30\left(nghìn.đồng\right)\)
Số tiền Lan mua thước là :
\(30:\dfrac{2}{3}=30.\dfrac{3}{2}=45\left(nghìn.đồng\right)\)
Số tiền còn lại là :
\(150-\left(30+45\right)=75\left(nghìn.đồng\right)\)
Số tiền Lan có thể mua 10 quyển tập là :
\(8.10=80\left(nghìn.đồng\right)\)
mà số tiền còn lại nhỏ hơn số tiền mua 10 quyển tập : \(75\left(nghìn.đồng\right)< 80\left(nghìn.đồng\right)\)
Vậy Lan không đủ tiền mua 10 quyển tập.
Số tiền Lan dùng để mua bút là :
150 000 \(\times\) \(\dfrac{1}{5}\) = 30 000 ( đồng )
Số tiền Lan dùng để mua thước là :
30 000 \(_{\times}\) \(\dfrac{2}{3}\) = 20 000 ( đồng )
Số tiền Lan còn lại là :
150 000 - 20 000 - 30 000 = 100 000 ( đồng )
Số tiền mua 10 quyển vở là :
8 000 \(\times\) 10 = 80 000 ( đồng )
Ta thấy : 80 000 < 100 000
Nên số tiền còn lại đủ để mua 10 quyển vở
Hok tot

Ta có: \(A=\dfrac{2n+3}{8n}\) nguyên
\(\Rightarrow4A=4\cdot\dfrac{2n+3}{8n}=\dfrac{8n+12}{8n}\) nguyên
\(\Rightarrow4A=1+\dfrac{12}{8n}=1+\dfrac{3}{2n}\)
Để 4A nguyên thì 3 ⋮ 2n
⇒ 2n ∈ Ư(3) = {1; -1; 3; -3}
Mà: n ∈ Z ⇒ không có n thỏa mãn
Tìm số nguyên n để thỏa A mãn điều gì vậy em?

\(A=92-\dfrac{1}{9}-\dfrac{2}{10}-...-\dfrac{92}{100}\)
\(=\left(1-\dfrac{1}{9}\right)+\left(1-\dfrac{2}{10}\right)+...+\left(1-\dfrac{92}{100}\right)\)
\(=\dfrac{8}{9}+\dfrac{8}{10}+...+\dfrac{8}{100}\)
\(=8\left(\dfrac{1}{9}+\dfrac{1}{10}+...+\dfrac{1}{100}\right)\)
\(B=\dfrac{1}{45}+\dfrac{1}{50}+...+\dfrac{1}{500}\)
\(=\dfrac{1}{5}\left(\dfrac{1}{9}+\dfrac{1}{10}+...+\dfrac{1}{100}\right)\)
=>\(\dfrac{A}{B}=\dfrac{8\left(\dfrac{1}{9}+\dfrac{1}{10}+...+\dfrac{1}{100}\right)}{\dfrac{1}{5}\left(\dfrac{1}{9}+\dfrac{1}{10}+...+\dfrac{1}{100}\right)}=8:\dfrac{1}{5}=40\)
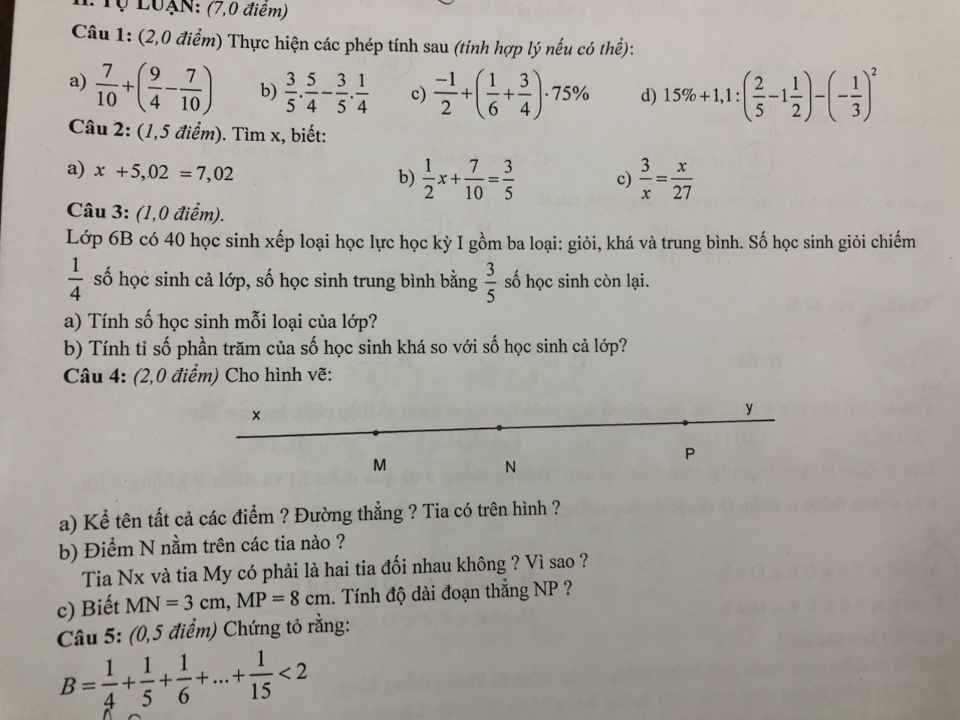
Ta có:
n + 2 = n + 1 + 1
Để (n + 2)/(n + 1) là số nguyên thì 1 ⋮ (n + 1)
n + 1 ∈ Ư(1) = {-1; 1}
n + 1 ∈ {-2; 0}