a, Ta có:

\(m_H=1,59\%.63=1\left(amu\right)\\ m_N=22,22\%.63=14\left(amu\right)\\ m_O=63-\left(1+14\right)=48\left(amu\right)\)

Đặt CTTQ:

 \(H_aN_bO_c\left(a,b,c:nguyên,dương\right)\\ a=\dfrac{1}{1}=1;b=\dfrac{14}{14}=1;c=\dfrac{48}{16}=3\\ \Rightarrow CTHH:HNO_3\)

Câu b)

\(m_O=16.3=48\left(amu\right)\\ m_{Fe}=160-48=112\left(amu\right)\\ Mặt.khác:m_{Fe}=56x\left(amu\right)\\ Nên:56x=112\\ \Leftrightarrow x=2\\ Vậy.CTHH:Fe_2O_3\)

Hình 5 đâu rồi em?

Tuỳ theo mức độ thấp như thế nào, nhưng nếu em cố gắng em có khả năng nâng 1 bậc học lực cả năm, thậm chí 2 bậc

mik đoán chắc là đc tại vì nó nhân hệ số mỗi kì

Nhờ mọi người giúp em câu b với.

lol

1A    

2C

3B

4D

5A

6A

Giả sử x;y;z đều chẵn

\(\Rightarrow x=2a;y=2b;z=2c\Rightarrow xyz=8abc⋮4\)

Nếu x;y;z đều lẻ => (x-y); (y-z); (z-x) chẵn

\(\Rightarrow\left(x-y\right)=2a;\left(y-z\right)=2b;\left(z-x\right)=2c\)

\(\Rightarrow\left(x-y\right)\left(y-z\right)\left(z-x\right)=8abc⋮4\)

Nếu trong 3 số x;y;z có ít nhất 1 số lẻ giả sử x lẻ  

=> xyz chẵn và \(xyz=2a\)

=> (y-z) chẵn và \(y-z=2b\)

\(\Rightarrow xyz\left(x-y\right)\left(y-z\right)\left(z-x\right)=\)

\(=2a.\left(x-y\right).2b.\left(z-x\right)=4ab\left(x-y\right)\left(z-x\right)⋮4\)

\(\Rightarrow xyz\left(x-y\right)\left(y-z\right)\left(z-x\right)⋮4\forall x;y;z\)

Nếu 1 trong 3 số x; y; z chia hết cho 3

\(\Rightarrow xyz\left(x-y\right)\left(y-z\right)\left(z-x\right)⋮3\)

Nếu không có số nào chia hết cho 3 ta có một số khi chia cho 3 dư 1 hoặc 2 => trong 3 số có 2 số đồng dư

=> 1 trong 3 số (x-y); (y-z); (z-x) có 1 số chia hết cho 3

\(\Rightarrow xyz\left(x-y\right)\left(y-z\right)\left(z-x\right)⋮3\)

\(\Rightarrow xyz\left(x-y\right)\left(y-z\right)\left(z-x\right)⋮3\forall x;y;z\)

Mà 3 và 4 là 2 số nguyên tố cùng nhau

\(\Rightarrow xyz\left(x-y\right)\left(y-z\right)\left(z-x\right)⋮3.4=12\forall x;y;z\)

a) A nguyên khi (12n + 17) ⋮ (3n + 1)

Ta có:

12n + 17 = 12n + 4 + 13

= 4(3n + 1) + 13

Để (12n + 17) ⋮ (3n + 1) thì 13 ⋮ (3n + 1)

⇒ 3n + 1 ∈ Ư(13) = {-13; -1; 1; 13}

⇒ 3n ∈ {-14; -2, 0; 12}

⇒ n ∈ {-14/3; -2/3; 0; 4}

Mà n là số nguyên

⇒ n ∈ {0; 4}

b) Để A là số nguyên thì ⋮ (10n + 9) (5n - 1)

Ta có:

10n + 9 = 10n - 2 + 11

= 2(5n - 1) + 11

Để (10n + 9) ⋮ (5n - 1) thì 11 ⋮ (5n - 1)

⇒ 5n - 1 ∈ Ư(11) = {-11; -1; 1; 11}

⇒ 5n ∈ {-10; 0; 2; 12}

⇒ n ∈ {-2; 0; 2/5; 12/5}

Mà n là số nguyên

⇒ n ∈ {-2; 0}

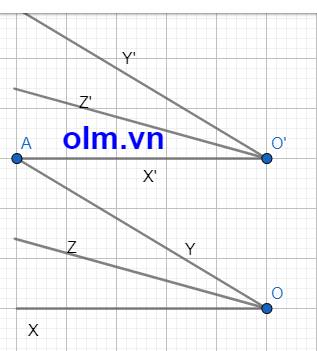
a,Kéo dài OY cắt O'X' tại A ta có: 

  \(\widehat{XOY}\) =  \(\widehat{XOA}\)  = \(\widehat{OAO'}\) (so le trong) (1)

   \(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)

Kết hợp (1) Và (2) ta có:

    \(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)

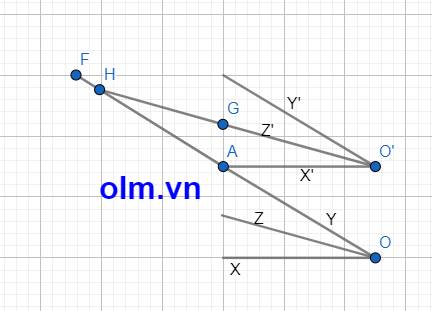
b, Kéo dài OY cắt O'Z' tại H 

             \(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY

             \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')

         Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)

               \(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\)  ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)

          ⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)

         ⇒ OZ // O'Z' (đpcm)

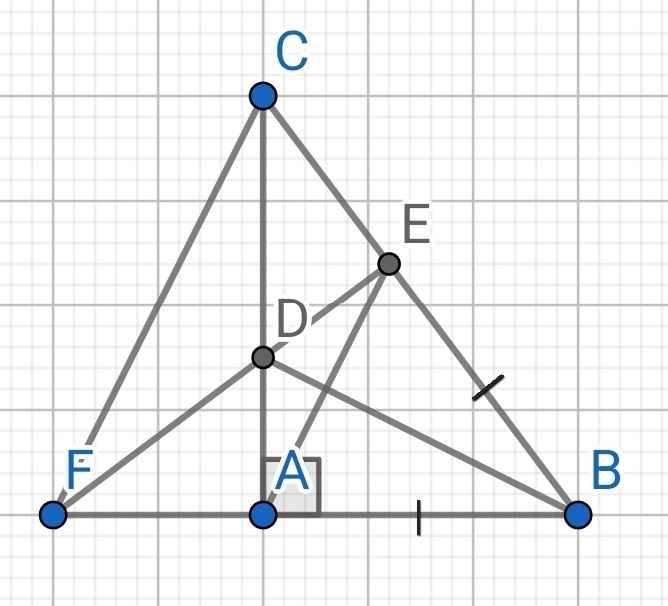 a) Xét ∆ABD và ∆EBD có:

AB = BE (gt)

∠ABD = ∠EBD (BD là tia phân giác của ABC)

BD là cạnh chung

⇒ ∆ABD = ∆EBD (c-g-c)

b) Do ∆ABD = ∆EBD (cmt)

⇒ AD = ED (hai cạnh tương ứng)

Lại do ∆ABD = ∆EBD (cmt)

⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)

⇒ ∠DAF = ∠DEC = 90⁰

Xét hai tam giác vuông: ∆DAF và ∆DEC có:

AD = ED (cmt)

∠ADF = ∠EDC (đối đỉnh)

⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)

⇒ AF = EC (hai cạnh tương ứng)

c) ∆BAE có:

AB = BE (gt)

⇒ ∆BAE cân tại B

⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2  (1)

Do AF = EC (cmt)

AB = BE (gt)

⇒ AF + AB = EC + BE

⇒ BF = BC

⇒ ∆BFC cân tại B

⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2  (2)

Từ (1) và (2) suy ra:

∠BEA = ∠BCF

Mà ∠BEA và ∠BCF là hai góc đồng vị

⇒ AE // CF