a) Nhận thấy \(\widehat{OBK}=\widehat{OAK}=90^o\) \(\Rightarrow\) Tứ giác OAKB nội tiếp đường tròn (OK).

Mặt khác \(\widehat{OHK}=90^o\) nên \(H\in\left(OK\right)\)

\(\Rightarrow\) 5 điểm A, B, O, K, H cùng thuộc đường tròn (OK).

b) Từ câu a) \(\Rightarrow\) Tứ giác OAHB nội tiếp 

\(\Rightarrow\widehat{IHB}=\widehat{IAO}\)

Từ đó dễ dàng chứng minh \(\Delta IHB~\Delta IAO\left(g.g\right)\)

\(\Rightarrow\dfrac{IH}{IA}=\dfrac{IB}{IO}\) \(\Rightarrow IA.IB=IH.IO\) (đpcm)

c) Gọi T là giao điểm của OK và AB.

Tính chất của 2 tiếp tuyến cắt nhau \(\Rightarrow OK\perp AB\) tại T

Tam giác OAK vuông tại A có đường cao AT nên \(OT.OK=OA^2\) (hệ thức lượng trong tam giác vuông)

Xét tam giác OTI và OHK, ta có:

\(\widehat{HOK}\) chung , \(\widehat{OTI}=\widehat{OHK}=90^o\)

 \(\Rightarrow\Delta OTI~\Delta OHK\left(g.g\right)\)

 \(\Rightarrow\dfrac{OT}{OH}=\dfrac{OI}{OK}\)

 \(\Rightarrow OT.OK=OH.OI\)

Mà \(OT.OK=OA^2\) (cmt) \(\Rightarrow OH.OI=OA^2\)

\(\Rightarrow OI=\dfrac{OA^2}{OH}\) là một hằng số 

\(\Rightarrow\) I thuộc đường tròn \(\left(O;\dfrac{OA^2}{OH}\right)\) cố định

Hơn nữa I nằm trên đường thẳng OH cố định nên I cố định

\(\Rightarrow\) AB đi qua I cố định.

khó thế con Phương kia

tịt

Bạn Lý Bình Minh không đăng linh tinh!

Nếu không, mình sẽ báo cáo!

Lời giải:

\(A=\frac{\sqrt{x}(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}+\frac{\sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}+3)}-\frac{4\sqrt{x}-6}{(\sqrt{x}-3)(\sqrt{x}+3)}\\ =\frac{\sqrt{x}(\sqrt{x}-3)+\sqrt{x}+3-(4\sqrt{x}-6)}{(\sqrt{x}-3)(\sqrt{x}+3)}\\ =\frac{x-6\sqrt{x}+9}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{(\sqrt{x}-3)^2}{(\sqrt{x}-3)(\sqrt{x}+3)}\\ =\frac{\sqrt{x}-3}{\sqrt{x}+3}\)

\(A=\dfrac{2021x+2022\sqrt{1-x^2}+2023}{\sqrt{1-x^2}}\)

\(A=2022+\dfrac{2021x+2023}{\sqrt{1-x^2}}\)

Xét \(\dfrac{2021x+2023}{\sqrt{1-x^2}}\)

\(\dfrac{2021x+2023}{\sqrt{1-x^2}}\ge2\sqrt{2022}\) 

\(\Rightarrow A\ge2022+2\sqrt{2022}\)

\(A\ge2\left(1011+\sqrt{2022}\right)\)

Dấu "=" xảy ra khi \(x=-\dfrac{2021}{2023}\)

\(\left\{{}\begin{matrix}8x^3y^3+27=18y^3\left(1\right)\\4x^2y+6x=y^2\left(2\right)\end{matrix}\right.\)

pt (2) \(\Leftrightarrow4x^2y^2+6xy=y^3\) (3)

Thế (3) vào (1), ta được \(8x^3y^3+27=18\left(4x^2y^2+6xy\right)\)

\(\Leftrightarrow8\left(xy\right)^3-72\left(xy\right)^2-108xy+27=0\) (4)

Đặt \(xy=t\) thì (4) thành

\(8t^3-72t^2-108t+27=0\)

\(\Leftrightarrow8t^3+12t^2-84t^2-126t+18t+27=0\)

\(\Leftrightarrow4t^2\left(2t+3\right)-42t\left(2t+3\right)+9\left(2t+3\right)=0\)

\(\Leftrightarrow\left(2t+3\right)\left(4t^2-42t+9\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=-\dfrac{3}{2}\\t=\dfrac{21\pm9\sqrt{5}}{4}\end{matrix}\right.\)

Xét \(t=-\dfrac{3}{2}\) \(\Rightarrow xy=-\dfrac{3}{2}\) . Thay vào (2), ta có:

\(y^3=4\left(xy\right)^2+6xy\) \(=4\left(-\dfrac{3}{2}\right)^2+6\left(-\dfrac{3}{2}\right)=0\)  

\(\Leftrightarrow y=0\) \(\Leftrightarrow x=0\)

Nếu \(t=\dfrac{21+9\sqrt{5}}{4}\) thì \(xy=\dfrac{21+9\sqrt{5}}{4}\). Thay vào (2), ta có:

\(y^3=4\left(\dfrac{21+9\sqrt{5}}{4}\right)^2+6\left(\dfrac{21+9\sqrt{5}}{4}\right)\) \(\Rightarrow y=...\Rightarrow x=...\)

Xét tương tự với \(t=\dfrac{21-9\sqrt{5}}{4}\)

Vậy ...

 Với lại bạn cần loại nghiệm \(x=y=0\) nhé vì nó không thỏa mãn pt (1).

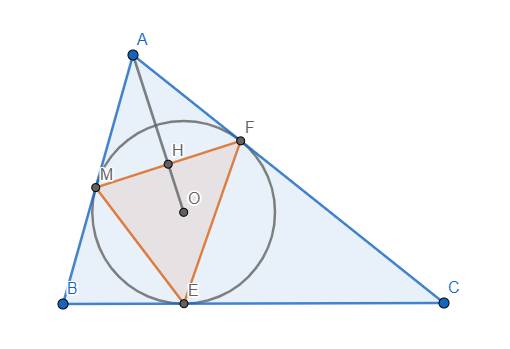
Gọi H là giao điểm của FM và OA.

Tính được \(AM=\dfrac{b+c-a}{2}\)

Tính được \(cos\widehat{BAC}=\dfrac{b^2+c^2-a^2}{2bc}\) rồi dùng 

\(MF=\sqrt{AM^2+AF^2-2AM.AF.cos\widehat{BAC}}\)

 \(=\sqrt{2AM^2\left(1-cos\widehat{BAC}\right)}\) 

 \(=MA\sqrt{2\left(1-\dfrac{b^2+c^2-a^2}{2bc}\right)}\)

 \(=MA\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}\)

 \(=\dfrac{b+c-a}{2}\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}\)

\(\Rightarrow\dfrac{MF}{MA}=\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}=J\)

\(\Rightarrow cos\widehat{MEF}=cos\widehat{MAH}=\dfrac{MH}{MA}=\dfrac{J}{2}\)

\(\Rightarrow sin\widehat{MEF}=\sqrt{1-cos^2\widehat{MAH}}\)

 \(=\sqrt{1-\dfrac{J^2}{4}}\) 

 \(=\sqrt{1-\dfrac{a^2-b^2-c^2+2bc}{4bc}}\)

 \(=\sqrt{\dfrac{\left(b+c\right)^2-a^2}{4bc}}\) \(=A\)

Ta cũng tính được \(ME=\dfrac{c+a-b}{2}\sqrt{\dfrac{b^2-\left(c-a\right)^2}{ca}}=\dfrac{c+a-b}{2}\sqrt{\dfrac{\left(b+c-a\right)\left(a+b-c\right)}{ca}}\)

\(EF=\dfrac{a+b-c}{2}\sqrt{\dfrac{c^2-\left(a-b\right)^2}{ab}}=\dfrac{a+b-c}{2}\sqrt{\dfrac{\left(c+a-b\right)\left(b+c-a\right)}{ab}}\)

\(\Rightarrow S_{MEF}=\dfrac{1}{2}EM.EF.sin\widehat{MEF}\) \(=...\)

 Điểm F ở câu a) với điểm N ở câu b) là những điểm gì thế bạn? Mình thấy trong đề không có định nghĩa các điểm này.